Определение 1.4. Функция  называется бесконечно большой (б.б.ф.) при
называется бесконечно большой (б.б.ф.) при 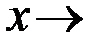
 , если для любого числа
, если для любого числа 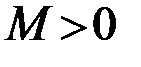 существует число
существует число 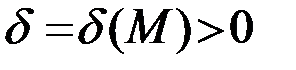 , такое что для всех
, такое что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 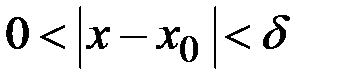 ,выполняется неравенство
,выполняется неравенство 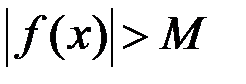 .
.
Записывают 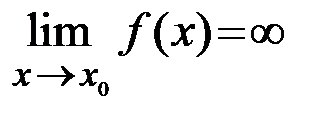 .
.
Всякая б.б. в окрестности точки  функция является неограниченной в этой окрестности.
функция является неограниченной в этой окрестности.
Определение 1.5. Функция  называется бесконечно малой (б.м.ф.) при
называется бесконечно малой (б.м.ф.) при 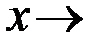
 , если
, если  .
.
Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми и обозначают греческими буквами 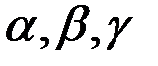 . Далее приведены основные теоремы о бесконечно малых функциях.
. Далее приведены основные теоремы о бесконечно малых функциях.
Теорема 1.5. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
Теорема 1.6. Произведение ограниченной функции на бесконечно малую функцию есть бесконечно малая функция.
Следствие 1.1. Так как всякая б.м.ф. ограничена, то из теоремы 2 вытекает, что произведение двух б.м.ф. есть бесконечно малая функция.
Следствие 1.2. Произведение б.м.ф. на число есть бесконечно малая функция.
Теорема 1.7. Частное от деления б.м.ф. на функцию, имеющую отличный от нуля предел, есть бесконечно малая функция.
Теорема 1.8. (о связи б.м. и б.б.) Если функция 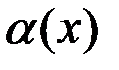 – бесконечно малая (
– бесконечно малая (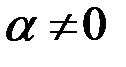 ), то функция
), то функция  есть бесконечно большая функция и наоборот: если функция
есть бесконечно большая функция и наоборот: если функция 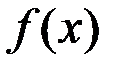 – бесконечно большая, то функция
– бесконечно большая, то функция  есть бесконечно малая функция.
есть бесконечно малая функция.
Теорема 1.9. (о представлении функции, имеющей конечный предел)
Если функция 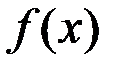 имеет предел, равный
имеет предел, равный  , то ее можно представить как сумму числа
, то ее можно представить как сумму числа  и бесконечно малой функции
и бесконечно малой функции 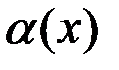 , то есть если
, то есть если  , то
, то 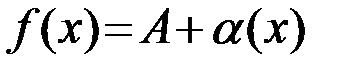 .
.
Теорема 1.10. (обратная)
Если функцию 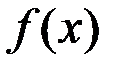 можно представить в виде суммы числа
можно представить в виде суммы числа  и бесконечно малой функции
и бесконечно малой функции 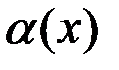 , то число
, то число  является пределом функции, то есть если
является пределом функции, то есть если 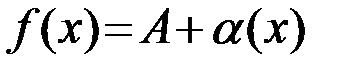 , то
, то  .
.
 2020-10-09
2020-10-09 439
439








