2020-10-09
142
Последовательность, не имеющая предела, называется расходящейся.
Теорема 1.1. Если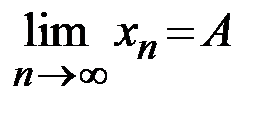 
, 
и, начиная с некоторого номера 
, выполняется неравенство 
, то 
.
Теорема 1.2. Если ,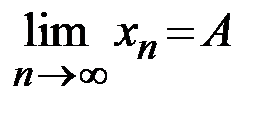 
и, начиная с некоторого номера , выполняется неравенство 
, то 
.
Теорема 1.3. (Вейерштрасса)
Всякая монотонная ограниченная последовательность имеет предел.
Предел функции
Рассматривается функция 
, определенная в некоторой (достаточно малой) окрестности точки 
, кроме быть может, самой точки . Сформулируем два определения предела функции в точке .
