Число  называется пределом функции
называется пределом функции  в точке
в точке  (или при
(или при 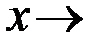
 ), если для любой последовательности допустимых значений аргумента
), если для любой последовательности допустимых значений аргумента  (
(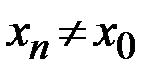 ), сходящейся к
), сходящейся к  (то есть
(то есть 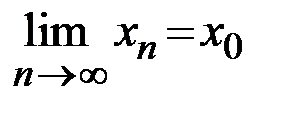 ), последовательность соответствующих значений функции
), последовательность соответствующих значений функции 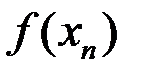 сходится к числу
сходится к числу  (то есть
(то есть 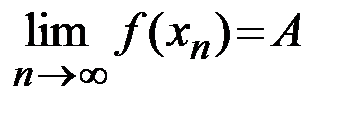 ).
).
В этом случае пишут 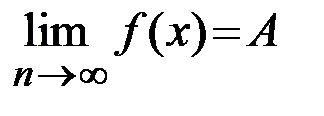 или
или 
 , при
, при 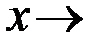
 .
.
Определение 1.2. (по Коши, на языке « 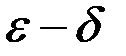 » )
» )
Число  называется пределом функции
называется пределом функции  в точке
в точке  (или при
(или при 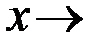
 ), если для любого сколь угодно малого числа
), если для любого сколь угодно малого числа  найдется такое число
найдется такое число  , что для всех
, что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 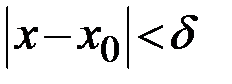 , выполняется неравенство
, выполняется неравенство  .
.
Записывают 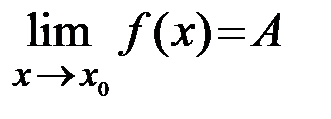 (см.рис. 6.1). Кратко определение предела функции записывается так:
(см.рис. 6.1). Кратко определение предела функции записывается так: 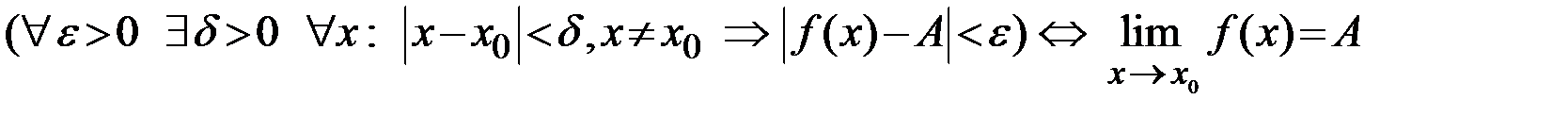 .
.
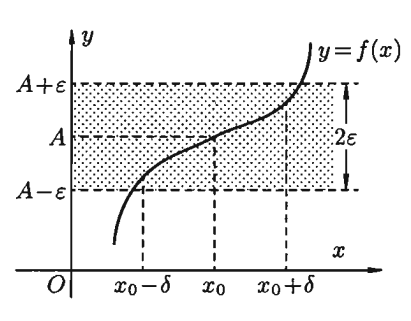
Рис. 1. 1
З а м е ч а н и е 1.1. Подразумевается, что 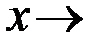
 определении предела функции
определении предела функции 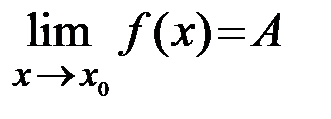 любым способом: оставаясь слева от точки
любым способом: оставаясь слева от точки  или справа от точки
или справа от точки  , или колеблясь около точки
, или колеблясь около точки  . В некоторых случаях возникает необходимость рассматривать односторонние пределы, то есть предел функции слева (при
. В некоторых случаях возникает необходимость рассматривать односторонние пределы, то есть предел функции слева (при 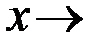
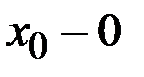 ) или справа (при
) или справа (при 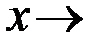
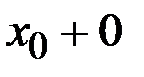 ) от точки
) от точки  .
.
Число  называется пределом функции
называется пределом функции  слева в точке
слева в точке  , если для любого сколь угодно малого числа
, если для любого сколь угодно малого числа  найдется такое число
найдется такое число  , что при всех
, что при всех  , выполняется неравенство
, выполняется неравенство  .
.
Записывают 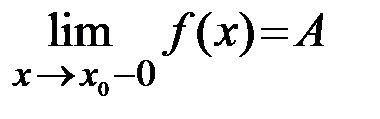 .
.
Число  называется пределом функции
называется пределом функции  справа в точке
справа в точке  , если для любого сколь угодно малого числа
, если для любого сколь угодно малого числа  найдется такое число
найдется такое число  , что при всех
, что при всех  , выполняется неравенство
, выполняется неравенство  .
.
Записывают 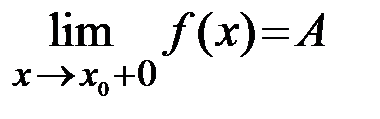 .
.
Теорема 1.4. ( существования предела функции в точке  ) Если
) Если 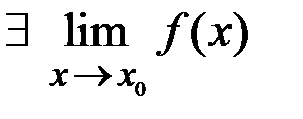 , то
, то  и
и  , причем
, причем 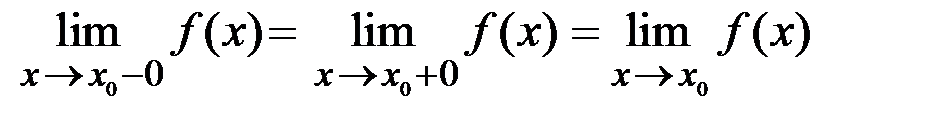 .
.
Верно и обратное: если  ,
,  и
и 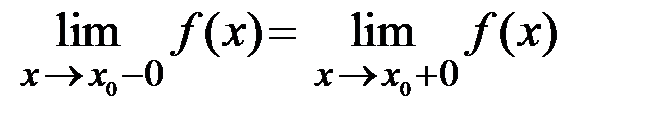 то
то 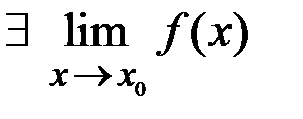 .
.
Пусть функция определена при 
Определение 1.3. (предела функции при 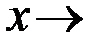
 )
)
Число  называется пределом функции
называется пределом функции  при
при 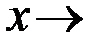
 , если для любого сколь угодно малого числа
, если для любого сколь угодно малого числа  найдется такое число
найдется такое число 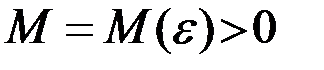 , что для всех
, что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 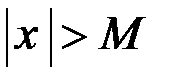 , выполняется неравенство
, выполняется неравенство  .
.
Записывают 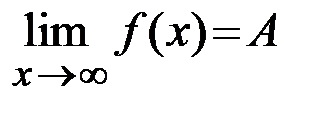 .
.
 2020-10-09
2020-10-09 445
445








