Введение
Целью изучения дисциплины «Математический анализ» является воспитание достаточно высокой математической культуры, привитие навыков современных видов математического мышления, обучение основным понятиям и методам математического анализа, необходимым для анализа и моделирования устройств, процессов и явлений при поиске оптимальных решений практических задач, методам обработки и анализа результатов численных экспериментов для экономических задач.
Для достижения поставленной цели решаются следующие задачи:
- самостоятельное изучение теоретического материала, построенного на основе четких формулировок и доказательство основных теорем; выработка способности проиллюстрировать самостоятельно изученный материал примерами и задачами;
- самостоятельное изучение истории появления наиболее важных понятий и результатов, а также пояснений об их приложениях к другим разделам математики и к другим наукам;
- закрепление самостоятельно изученного теоретического материала и выработка умения самостоятельно решать задачи для последующего применения математических методов в различных приложениях.
Студент по результатам освоения дисциплины «Математический анализ» должен обладать способностью выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы.
В результате самостоятельного освоения дисциплины студент должен:
- знать основные понятия, определения и методы исследования объектов
с помощью теорем и формул различных разделов курса математического анализа;
- уметь: четко формулировать и доказывать основные положения курса
математического анализа, решать задачи и примеры по различным разделам математического анализа с доведением решения до практического приемлемого результата (формулы, числа, графика, качественного вывода и т.п.), уметь при решении задач выбирать необходимые вычислительные методы и средства (ПЭВМ, таблицы и справочники); самостоятельно изучать научную литературу по линейной алгебре;
- иметь представление о численных алгоритмах решения
математических и прикладных задач его профессиональной области.
ПРЕДЕЛ ФУНКЦИИ
Понятие функции
Пусть даны два непустых множества 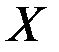 и
и 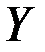 .
.
Функция – это соответствие  , которое каждому элементу
, которое каждому элементу 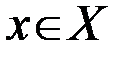 сопоставляет единственный элемент
сопоставляет единственный элемент 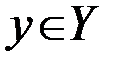 . Область определения функции – множество
. Область определения функции – множество 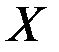 , которое обозначается
, которое обозначается 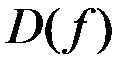 или кратко
или кратко 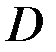 . Множество значений функции – множество
. Множество значений функции – множество 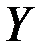 , которое обозначается
, которое обозначается 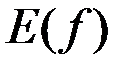 или
или 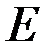 .
.
Чтобы задать функцию  необходимо указать правило, позволяющее, зная
необходимо указать правило, позволяющее, зная 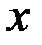 , находить
, находить 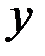 . Если элементами множеств
. Если элементами множеств 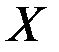 и
и 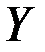 являются действительные числа, то функция называется числовой функцией и записывается
являются действительные числа, то функция называется числовой функцией и записывается  . Переменная
. Переменная 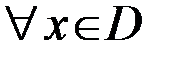
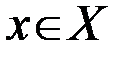 называется аргументом, а
называется аргументом, а 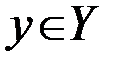 – значением функции, соответствующим заданному значению аргумента
– значением функции, соответствующим заданному значению аргумента 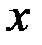 .
.
Графиком функции  называется множество всех точек плоскости
называется множество всех точек плоскости 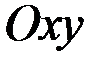 с координатами
с координатами 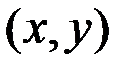 , для каждой из которых
, для каждой из которых 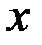 является аргументом, а
является аргументом, а 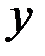 – значением функции.
– значением функции.
Наиболее часто встречаются три способа задания функции: аналитический (в виде одной или нескольких формул), графический (в виде графика) и табличный (в виде ряда отдельных значений аргумента и соответствующим им значений функции).
Далее вводятся некоторые характеристики для функции  , определенной на множестве
, определенной на множестве 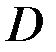 .
.
1. Функция называется четной, если 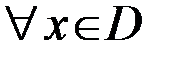 выполняются условия
выполняются условия 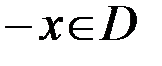 и
и  .
.
2. Функция  , называется нечетной, если
, называется нечетной, если 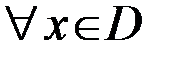 выполняются условия
выполняются условия 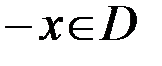 и
и 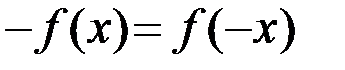 .
.
3. Функция называется возрастающей на множестве 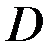 , если
, если 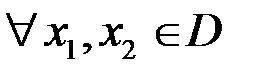 , таких что
, таких что 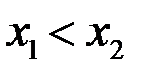 выполняется условие
выполняется условие 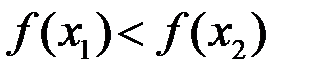 (если выполняется условие
(если выполняется условие 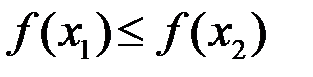 , то функция называется неубывающей).
, то функция называется неубывающей).
4. Функция называется убывающей на множестве 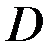 , если
, если 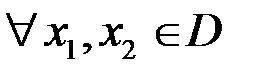 , таких что
, таких что 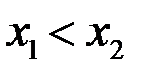 выполняется условие
выполняется условие 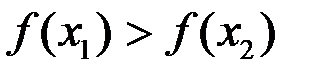 (если выполняется условие
(если выполняется условие 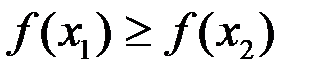 , то функция называется невозрастающей).
, то функция называется невозрастающей).
Возрастающие, неубывающие, убывающие и невозрастающие функции называются монотонными, а возрастающие и убывающие – строго монотонными на множестве 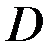 функциями.
функциями.
5. Если существует такое число  , что
, что 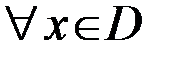 выполняется неравенство
выполняется неравенство 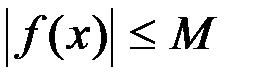 , то функция
, то функция  называется ограниченной на множестве
называется ограниченной на множестве 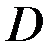 .
.
6. Если существует такое число 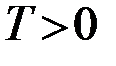 , что
, что 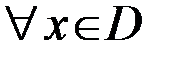 значение
значение  и
и 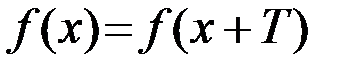 , то функция
, то функция  называется периодической на множестве
называется периодической на множестве 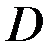 .
.
Пусть задана функция  с областью определения
с областью определения 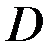 и множеством значений
и множеством значений 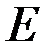 . Если введено соответствие, которое каждому элементу
. Если введено соответствие, которое каждому элементу 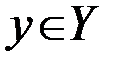 сопоставляет единственный элемент
сопоставляет единственный элемент 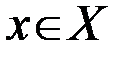 , то определена обратная функция
, то определена обратная функция 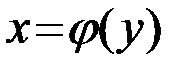 с областью определения
с областью определения 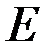 и множеством значений
и множеством значений 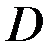 . Записывается в виде
. Записывается в виде  . Если ввести переобозначения: аргумент обратной функции обозначить символом
. Если ввести переобозначения: аргумент обратной функции обозначить символом 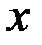 , а значение – символом
, а значение – символом 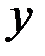 , то обратная функция принимает вид
, то обратная функция принимает вид 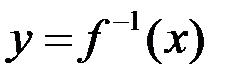
Для функции  определена обратная
определена обратная 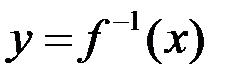 тогда и только тогда, когда
тогда и только тогда, когда  определяет взаимно-однозначное соответствие между множествами
определяет взаимно-однозначное соответствие между множествами 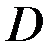 и
и 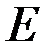 . То есть любая строго монотонная функция имеет обратную.
. То есть любая строго монотонная функция имеет обратную.
Пусть задана функция 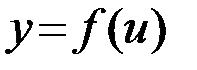 с областью определения
с областью определения 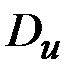 и множеством значений
и множеством значений 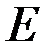 , а функция
, а функция 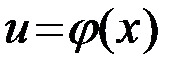 с областью определения
с областью определения 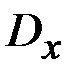 и множеством значений
и множеством значений 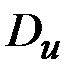 , то есть на множестве
, то есть на множестве 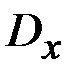 определена сложная функция
определена сложная функция  (или функция от функции, или суперпозиция заданных функций).
(или функция от функции, или суперпозиция заданных функций).
Числовые последовательности. Предел последовательности.
Под числовой последовательностью 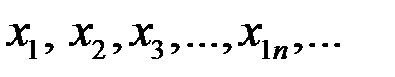 понимается функция
понимается функция 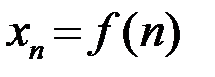 , заданная на множестве натуральных чисел
, заданная на множестве натуральных чисел  . Кратко последовательность обозначается в виде
. Кратко последовательность обозначается в виде 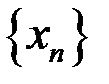 или
или  . Число
. Число 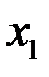 называется первым членом последовательности, число
называется первым членом последовательности, число 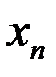 называется общим или
называется общим или 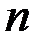 -м членом последовательности.
-м членом последовательности.
Последовательность называется ограниченной, если существует такое число  , что
, что  выполняется неравенство
выполняется неравенство  .
.
Последовательность называется возрастающей ( или неубывающей), если  выполняется условие
выполняется условие 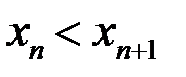 (или
(или 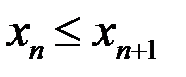 ). Эти последовательности называются монотонными.
). Эти последовательности называются монотонными.
Число  называется пределом последовательности
называется пределом последовательности 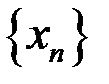 , если для любого сколь угодно малого числа
, если для любого сколь угодно малого числа  найдется такое натуральное число
найдется такое натуральное число  , что при всех
, что при всех 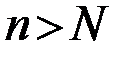 выполняется неравенство
выполняется неравенство 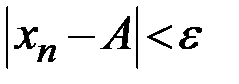 .
.
Говорят также, что последовательность 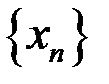 сходится к
сходится к  (является сходящейся) и записывают
(является сходящейся) и записывают 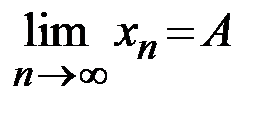 .
.
Кратко определение предела последовательности записывается так:
 .
.
 2020-10-09
2020-10-09 145
145







