Синусоидалы ток тізбегіндегі индуктивтілік 3 страница

 

берілсін, ал ізделулі шама болып 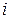 ток саналады. Осында, синусоидалы токтың қалыптасқан режимі қарастырылғандықтан, осы дифференциалды теңдеудің шешімі келесі түрдегі синусоидалы форманы беру тиіс

 

                          

 

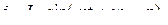
мұндағы 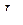 және 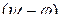 – белгісіз токтың әрі амплитудасы мен бастапқы фазасы.

Алдынғы параграфқа сәйкес берілген синусоидалы кернеу U _m 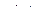 комплекстік функциясымен бейнеленеді, ал ізделулі синусоидалы ток I _m  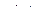комплекстік функциясымен; кернеу мен токтың комплекстік амплитудалары келесіге тең

 

U _m = U _m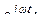

I _m = I _m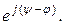

 

(3.4) теңдеуіндегі синусоидалы функцияларды қосу, дифференциалдау және интегралдау, комплекстік функциялардың жорымал бөліктері үшін сондай математикалық операцияларымен алмастырылады

 

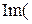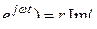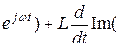U _m I _m 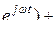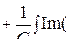I _m

I _m 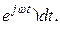                                                         (3.5)

 

Комплекстік функциялардың жорымал бөлігі бойынша операциялар алынған нәтижеден жорымал бөлігін шығару арқылы комплекстік функциялардың өздері бойынша операцияларға алмастырылуы мүмкін. Бұл қосу, операцияларының 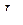 символдық операциясы бойынша коммутативтілігімен түсіндіріледі 

 

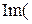U _{m .}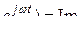

 

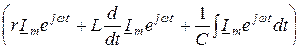Алынған теңдеу уақыттың кез-келген мерзімі үшін қанағаттандырады. Сондықтан жорымал бөлік алынатын, жақшаның ішіне еңгізілген комплекстік өрнек бір-біріне тең болу керек. Дифференциалдау және интегралдау жүргізіп, келесіні аламыз

 

                   U _m 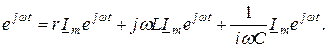         (3.6)

 

(3.6) теңдеудің барлық бөліктерін 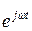 көбейткішке қысқарту нәтижесінде комплекстік алгебралық теңдеу шығады

 

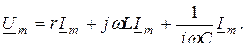                                         (3.7)

 

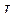 тогы жақшаның сыртына шығарылуы мүмкін. Осы кезде, қарастырылатын электрлік тізбектің комплекстік кедергісі үшін шартты белгі еңгізіледі

 

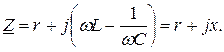                                                            (3.8)

 

Сондықтан комплекстік амплитудалар үшін Ом заңын өрнектейтін теңдеуді

 

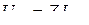                                                                                         (3.9)

 

аламыз.

Теңдеудің екі бөлігін 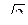 бөліп, комплекстік нақты мәндері үшін Ом заңын аламыз

 

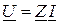                             .                                            (3.10)

Комплекстік нақты синусоидалы ток (комплекстік ток) – модулі мен аргументі, сәйкесінше нақты синусоидалы токқа және оның бастапқы фазасына тең комплекстік шама. Сондықтан, электрлік тізбектің комплекстік кедергісі берілген тізбектің комплекстік кернеуінің сол тізбектегі комплекстік токқа қатынасына тең.

(3.8) өрнегіндегі 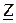 комплекстік кедергі алгебралық түрінде келтірілген. Осы шаманы тригонометриялық және көрсеткіштік (полярлық) түрлерінде көрсетейік

 

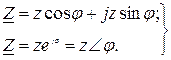                                                                  (3.11)

 

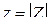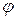мұндағы  – тізбектің толық кедергісін көрсетілген  комплекстік санның модулі, ал  –  комплекстік санның аргументі

 

 

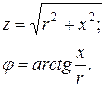
(3.9) негізінде токтың комплекстік амплитудасы  

 

 

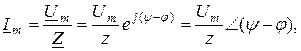
мұндағы 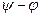 тоқтың бастапқы фазасы. Сондықтан, ізделулі ток тригонометриялық түрде былай жазылады

 

 

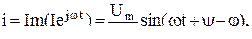
және ол алдында алынған нәтижемен сәйкес келеді (§ 2.7 қара).

 3.5 суретінде комплекстік жазықтықта (3.1) теңдеуін геометриялық түрі берілген. (3.5, а) суреті бойынша тізбектің реактивті кедергісі индуктивті сипатқа ие (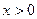) және ток фаза бойынша кернеуден қалып тұрады (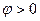). (3.5, б) суреті бойынша тізбектің реактивті кедергісі сиымдылықты сипатқа ие (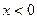) және ток фаза бойынша кернеуден озып тұрады ().

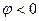Тізбектің таза реактивті жағдайы кезінде (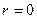), егер тізбектің кедергісі индуктивті болса, ток кернеуден фаза бойынша  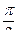бұрышына қалып тұрады, ал тізбектің кедергісі сиымдылықты болса ток кернеуден фаза бойынша  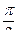бұрышына озып тұрады.

 

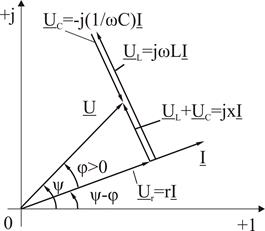
а)

 

 

                

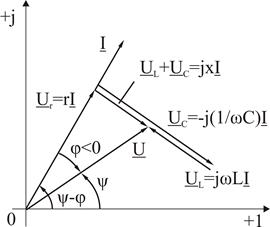
б)

 

  3.5 Сурет − 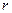, , 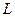 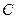бірізді тізбегі үшін  векторлы  диаграмма,

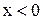  кезінде

 

3,5 суретінде келтірілген векторлық диаграммалардан келесіні көреміз

 

,

 

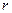–  кедергісіндегі кернеу ( 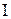тогымен фаза бойынша сәйкес келеді),

 

;

 

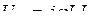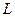–  индуктивтілігі кернеу ( 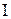 тогынан  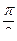бұрышына озып тұр) және

 

;

 

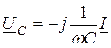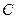– сиымдылықтағы кернеу ( 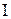 тогынан  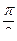бұрышына қалып тұр).

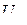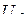,  және 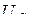 векторларының геометриялық қосындысы тізбекке жұмсалған кернеуді береді

 

.

 

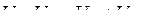Катеттері болып 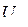 и 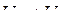, ал гипотенузасы болып  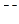саналатын тікбұрышты үшбұрышты кернеулер үшбұрышы деп аталады;  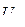және 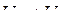 сәйкесінше, кернеудің активті және реактивті құраушылары болып келеді.

Егер осы үшбұрыштың барлық жақтарын – векторларын 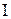 векторына бөлсе, онда кернеулер үшбұрышына сәйкес кедергілер үшбұрышы шығады және ол сағат тілі бойынша  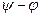бұрышына бұрылған болады.

Кедергілер үшбұрышы (3.11) теңдеуінің геометриялық түрін көрсетеді. Оның қалпы 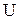 және 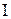 бастапқы фазалардан тәуелді емес;  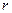кедергісі комплекстік жазықтықтың оң бағытта нақты бөлігінде салынады, ал  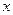реактивті кедергісі таңбасынан тәуелді жорымал бөліктің оң (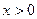) немесе кері (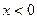) бағытында (3.6, а және б сурет) салынады.

 

                       

 

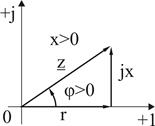
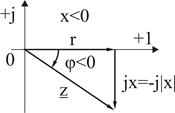
Кедергілер үшбұрышы                         Кедергілер үшбұрышы

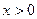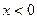           кезде                                                   кезде

                                              

                                          3.6 Сурет

 

 Кедергілер үшбұрышындағы 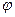 бұрышы  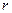катетынан  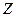гипотенузасына қарай саналады, кернеулер үшбұрышы үшін  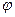бұрышы  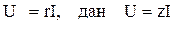қарай саналады.

3.2.2 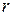,  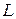және 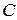 параллель қосылуы  

Комплексті амплетудаларға пропорционал комплекстік нақты мәндері үшін жазумен шектеліп, Кирхгофтың бірінші заңына сәйкес келесіні аламыз

 

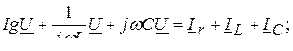                                          (3.12)

 

мұндағы  – кедергісіндегі ток (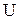  кернеуі мен фаза бойынша сәйкес келеді);

 

;

 

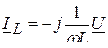индуктивтіліктегі ток (кернеуден 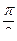 бұрышына қалып тұрады);

 

;

 

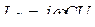сиымдылықтағы тоқ (кернеуден 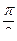 бұрышына озып тұрады)

 

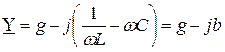                   ,                                 (3.13)

өрнегі қарастырылатын тізбектің толық өткізгіштігін көрсетеді. 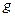 және 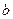 тізбектің активті және реактивті өткізгіштіктері

 

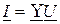                                        ,                                              (3.14)

               

теңдеуі комплекстік түрдегі Ом заңын көрсетеді. Сондықтан, электрлік тізбектің комплекстік тогының, оның шықпаларындағы комплекстік кернеуге қатынасы сияқты анықталады. 

Комплекстік өткізгіштің тригонометриялық және көрсеткіштік (полярлық) түрінде жазылуы

 

 

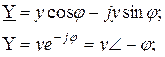
мұндағы 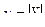 – тізбектің толық өткізгіштігін көрсететін  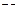комплекстік санның модулі, ал (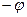) –  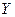комплекстік санының аргументі

 

 

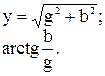
(3.14) негізінде  комплекстік  ток келесіге тең

 

 

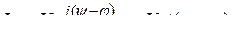
және ол синусоидалы токқа сәйкес келеді

 

 

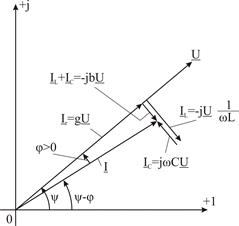
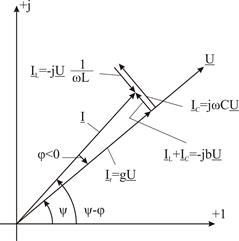
 (3.7) суретінде комплекстік жазықтықта (3.12) теңдеуінің геометриялық түрі берілген. 3.7, а суреті бойынша тізбектің реактивті өткізгіштігі индуктивті сипатқа ие (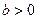) және ток фаза бойынша кернеуден қалып тұрады (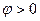). 3.7, б суреті бойынша тізбектің реактивті өткізгіштігі сиымдылықтық сипатқа ие (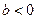) және ток фаза бойынша кернеуден озып тұрады().

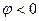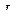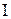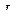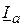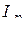Катеттері болып  және (), ал гипотенузасы болып  саналатын тікбұрышты үшбұрышты токтар үшбұрышы деп аталады;  және () сәйкесінше,  және  активті және реактивті құраушылары болып келеді.

 

         

 

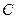, ,  параллель тізбек үшін  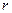   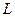   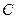  , ,  параллель тізбек үшін

векторлық диаграмма                                векторлық диаграмма

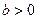        кезінде  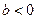                                           кезінде

 

3.7 Сурет

 

Егер осы үшбұрыштың барлық жақтарын – векторларын 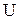 векторына бөлсе, онда токтар үшбұрышына сәйкес және  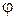бұрышына сағат тілі бойынша бұралған өткізгіштіктер үшбұрышы шығады. Өткізгіштіктер үшбұрышы (3.13) өрнегінің геометриялық түрін көрсетеді:  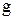өткізгіштігі комплекстік жазықтықтың оң бағытта нақты бөлігінде салынады, ал  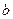реактивті өткізгіштігі таңбасынан тәуелді жорамал бөліктің оң (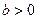) немесе кері (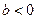) бағытында (3.8, а және б сурет) саналады.

                  

 

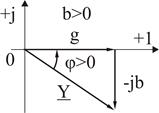
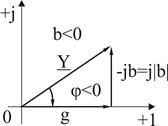
Өткізгіштіктер үшбұрышы                  Өткізгіштіктер үшбұрышы

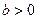           кезінде  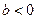                                      кезінде

 

3.8 Сурет

Өткізгіштіктер үшбұрышындағы 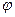 бұрышы  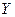гипотенузасынан  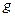катетына қарай саналады, токтар үшбұрышы үшін  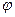бұрышы  деп 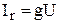 қарай саналады.

 3.1 кестесінде тізбектің негізгі элементтерінің жалпы түрде (дифференциалды, интегралды) теңдеулері берілген және синусоидалы режим кезінде тригонометриялық және комплекстік түрлері.

3.1 Кесте – Тізбек элементтерінің теңдеулері

Элемент	Жалпы түрі	Синусоидалы режим
		Тригонометриялық түрі	Комплекстік түрі
Кедергі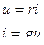
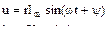
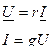
Индуктивтілік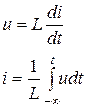
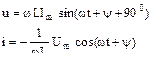
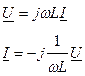
Сиымдылық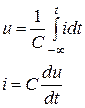

 

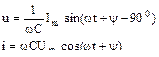
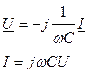
Индуктивтілік элементтің комплекстік кедергісі 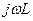 тең, ал сиымдылықтық элементтің комплекстік кедергісі  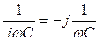тең екеніне назар аудару керек;сәйкесінше комплекстік өткізгіштіктер  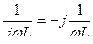және .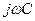

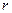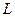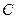, ,  элементтерінің әртүрлі қосылуы кезінде тізбектің комплекстік кедергілері мен өткізгіштіктері келтірілген.

 

 

 

3.2 Кесте – Комплекстік қарсы тұрудың көрсеткіші

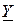Тізбек	бірізді қосылғанда	параллель қосылғанда

 

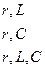
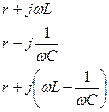
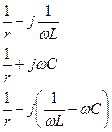
3.3 Тізбек бөлігінің кедергілері мен өткізгіштіктері арасындағы тәуелділік

Тізбектің кез-келген бөлігінің  комплекстік кедергісі белгілі болса, жазудың комплекстік түрін қолданып тізбек бөлігінің комплекстік өткізгіштігі

 

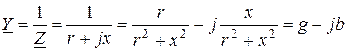        .                  (3.15)

 

Сонымен қатар, тізбек бөлігінің комплекстік өткізгіштігі белгілі болса

 

 

онда,  сол бөліктің комплекстік кедергісі

 

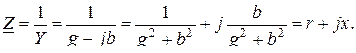                            (3.16)

 

(3.15) және (3.16) өрнектері, 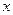 реактивті кедергі мен  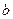реактивті өткізгіштік тізбектің бір бөлігі кезінде бірдей таңбаға ие екенін көрсетеді.

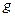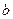Сонымен қатар, өткізгіштіктің әр қосылғышы (  және ) активті және де реактивті кедергілерден ( 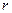 және 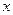) тәуелді болады.

 

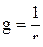және ,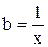

 

қатынастары жеке жағдайларда ғана әділетті, мысалы 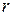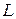,  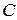элементтері жеке қарастырылған кезде