Типовые формы уравнений ОУ, управляемость и наблюдаемость, теоремы Калмана

Метод пространства состояний (метод переменных состояния) основан на понятии "состояние системы". Состояние динамической системы описывается совокупностью физических переменных x_i(t),..., x_n(t), характеризующих поведение системы в будущем при условии, если известно состояние в исходный момент времени и приложенные к системе воздействия.

В общем случае нелинейной системы, описание в переменных состояния имеет вид

. (6)

Если функции f₁, f₂,..., f_n линейны относительно переменных x₁, x₂,..., x_n, u₁, u₂,..., u_n и не зависят от времени t, то их можно привести к виду

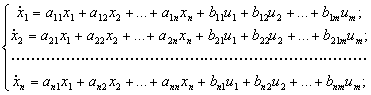. (7)

В матричной форме выражение (7) имеет вид

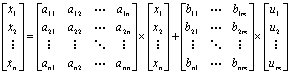. (8)

Такое выражение называется уравнением динамики для многомерной системы (u > 1), а в более компактном виде оно записывается через матричные операторы

. (8a)

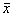где и 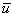вектор-столбцы, содержащие все переменные состояния и входные сигналы соответственно;

A - матрица динамики (состояния) объекта или системы размерностью n x n, (n - размерность вектора x);

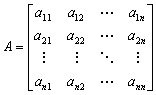
В — матрица управления (входа) размерностью n x m, (m — размерность вектора и), в случае одномерных систем матрица управления - вектор-столбец;

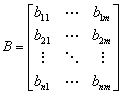
Для полного описания системы в пространстве состояний к уравнениям динамики (8) или (8 а) необходимо добавить уравнения, устанавливающие связи между переменными состояния x₁,..., x_п и выходными переменными y₁,...,y_r между входными u₁,..., u_m сигналами и выходными переменными y₁,...,y_r. Эта связь выражается в виде системы линейных алгебраических уравнений:

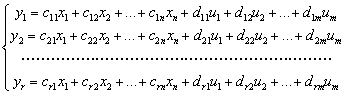; (9)

или в векторно-матричной форме, называемой уравнением выхода

, (9a)

где 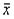- матрица-столбец выходных сигналов системы;

C - матрица выхода размерностью r x n, (r - размерность вектора y), в случае одномерных систем матрица выхода - вектор строка;

;

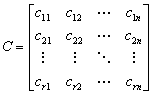D - матрица обхода (компенсации или усиления по входу), связывающая между собой входные и выходные сигналы. В реальных системах чаще всего такая связь отсутствует. Размерность матрицы обхода r x m. Для одномерных систем размерность матрицы обхода (1 x 1).

Для одномерных систем описание в пространстве состояний выглядит следующим образом

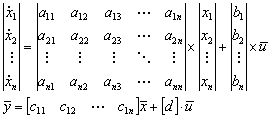. (10)

Таким образом, описание САУ в пространстве состояний выглядит как система двух уравнений в векторно матричной стандартной форме Коши

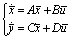. (11)

Выражению (11) соответствует условная структурная схема, изображенная на рис. 2.

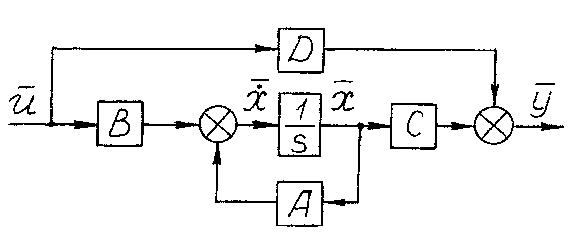
Рис. 2. Условная структурная схема многомерной САУ описанной уравнениями в пространстве состояний.

Описание системы управления в пространстве состояний удобно тем, что позволяет проводить анализ САУ на такие важные свойства как управляемость и наблюдаемость.

Понятие управляемость связано с возможностью приведения системы в заданное состояние с помощью входных или управляющих воздействий.