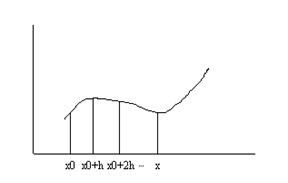
Пусть для функции y=f(x) заданы значения y i= f(xi) для равноотстоящих значений независимой переменной xi=x 0+ i*h (i=0,n), где h - шаг интерполяции.
Требуется подобрать полином Pn(x) степени не выше n, принимающий в точках xi значения Pn(xi)=yi (i=0,n)
Ньютон решил поставленную задачу:
Pn(x)=y 0+ q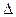 y +
y +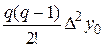 +
+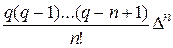 y0,
y0,
где q= 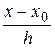 .
.
Эта формула называется первой интерполяционной формулой Нью-тона.
|
q= 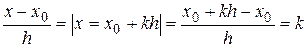 ,
,
где k - число шагов, необходимых для достижения точки x, исходя из точки x 0.
Рассмотрим частные случаи n= 1 или n= 2:
n= 1 P 1 (x)=y 0+ q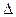 y 0 – линейное интерполирование
y 0 – линейное интерполирование
n= 2 P 2 (x)=y 0+ q 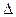 y 0+
y 0+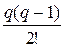
 2 y 0–параболическое (квадратичное) интерполирование
2 y 0–параболическое (квадратичное) интерполирование
Пример: необходимо построить интерполяционный полином Ньютона для функции y= 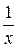 на отрезке
на отрезке 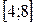 c h= 1
c h= 1
| X | |||||
| Y | 0.25 | 0.2 | 0.167 | 0.143 | 0.125 |
Горизонтальная таблица разностей.
| x | y | 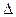 y y
| 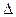 2y 2y
| 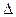 3y 3y
| 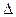 4y 4y
|
| 0.25 | -0.05 | 0.017 | -0.008 | 0.005 | |
| 0.2 | -0.033 | 0.009 | -0.003 | ||
| 0.167 | -0.024 | 0.006 | |||
| 0.143 | -0.018 | ||||
| 0.125 |
Т.о., при наличии 5 точек максимальный порядок существующей конечной разности =4, максимальная степень полинома =4.
P 4 (x)=y 0+ q 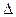 y 0+
y 0+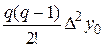 +
+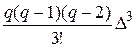 y0+
y0+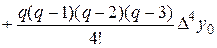
Как пользоваться формулой?
Допустим, необходимо определить значение в точке x= 4.4
Узловые точки x 0=4, h= 1,тогда q= 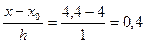
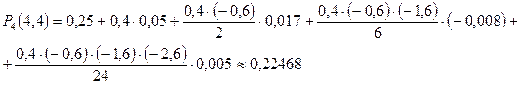 Точное значение =0.22727.
Точное значение =0.22727.
 2014-02-04
2014-02-04 539
539