2014-02-04
401
Является модификацией метода итераций. Основная идея заключается в том, что при вычислении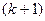 
-го приближения 
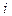-го корня используются уже вычисленные 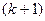приближённые корни 
.
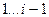Дано: 
, 
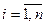
Выбираем начальное приближение:
На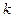 
-том шаге, согласно Зейделю строим приближение по следующим формулам:
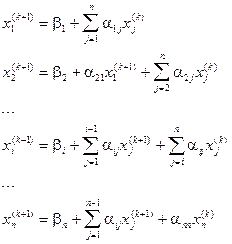
1. Метод Зейделя даёт полную сходимость по сравнению с методом итерации, но приводящий к громоздким вычислениям.
2. Теорема: Для существования единственного решения системы сходимости метода Зейделя достаточно выполнение хотя бы одного из двух условий:
1) 
,
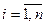
2) матрица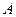 
- симметричная положительно определённая (все её соответственно значения положительны)
