Модели с частично распределенными параметрами

Модели с распределенными параметрами сложны и представляют вычисли­тельные трудности при их реализации. При этом не всегда бывает необходимо иметь распределение параметров микроклимата в моделируемом объекте по всем осям координат.

Например, в помещениях малой площади с равномерно распределенными ис­точниками вредности достаточно анализировать распределение того или иного параметра только по одной из трех координат, совпадающей с высотой поме­щения.

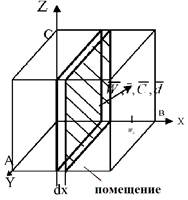Рис.2.2. К постановке задачи модели с частично распределенными парметрами. Параметры с чертой - средние по площади АС

В подобных случаях говорят о модели с частично распределенными пара­метрами (по одной или двум осям координат). В качестве такой модели продол­жим рассмотрение принятого выше примера - системы уравнений для движу­щегося потока жидкости. Уравнение движения для проекции на ось х имеет вид

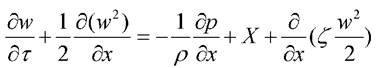(2.7)

где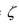- коэффициент потери энергии потока при движении. Уравнение сплошности потока

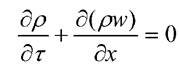(2.8)

Уравнение баланса тепловой энергии

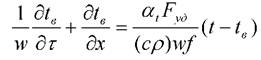(2.9)

где:

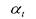-коэффициент теплообмена, Вт/м2 град;

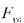-площадь поверхности теплообмена (ограждений), отнесенная к 1 м длины

пути воздуха, м;

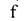-площадь поперечного сечения движущегося потока, м2;

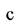-удельная теплоемкость воздуха, кДж/кг град;

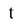-средняя по площади температура поверхностей, град.

Система уравнений дополняется граничными и начальными условиями. В при­веденной модели используются коэффициент обмена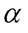и потерь энергии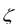, что упрощает задачу расчета. Следует иметь в виду, что эти коэффициенты связаны с реальными процессами формирования микроклимата. Поэтому их значения опре­деляют экспериментально или расчетом по более сложным трехмерным моделям..

2.2.3. Модели с сосредоточенными параметрами Такие модели наиболее распространены в инженерной практике, что связано с их простотой и доступностью реализации. Суть модели состоит в том, что все ве­личины в помещении принимаются средними по его объему. Таким образом рас­пределенные в общем случае параметры микроклимата концентрируются в одной точке, поэтому такие модели называют еще точечными. Для точечных моделей характерны следующие упрощения:

-равномерное распределение лучистых тепловых потоков пропорционально площади поверхности ограждений;

-одинаковая средняя температура поверхностей ограждений (радиационная температура);

-одинаковая средняя по объему температура воздуха; -одинаковая средняя концентрация вредных веществ в объеме помещения; -одинаковые и постоянные коэффициенты переноса (теплообмена, массооб- мена).

Точечные модели состоят из алгебраических уравнений и предназначены, как правило, для ручного счета. С их помощью определяют теплопотери и тепло- поступления в помещение, выделение вредностей, определение установочной производительности и решают широкий круг других задач обеспечения микро­климата.

Вместе с тем, подобные модели могут быть предназначены для решения неста­ционарных задач формирования микроклимата и поэтому включают уравнения в дифференциальной форме. В качестве примера рассмотрим модель формирования концентрации газовой вредности в помещении, известную как уравнение возду­хообмена (подробно см.раздел 6.3).

Уравнение баланса вредности включает поступление и расход вредности за бесконечно малый промежуток времени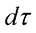. При этом дисбаланс вредности вы­зывает изменение концентрации:

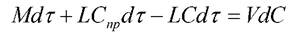(2.10)

где:

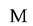-масса газовой вредности, поступающей в помещение, мг/ч;

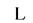-расход приточного воздуха, м3/ч;

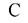-концентрация вредности в воздухе помещения, мг/м3;

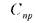-концентрация вредности в приточном воздухе, мг/м3;

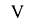-объем помещения,м3.

Уравнение (2.10) написано для случая, когда температура приточного и уходя­щего воздуха равны.

В помещениях большого объема имеет место выраженное распределение пара­метров микроклимата прежде всего по высоте. В этом случае, не прибегая к при­влечению более сложных моделей с полностью или частично распределенными параметрами, можно решить задачу приближенно с помощью точечной модели.

Решение состоит в выделении в объеме помещения двух зон (см.рис.2.3),для каждой из зон составляется уравнения баланса вредностей, которые дополняют уравнениями тепло-массообмена на границе раздела зон. Подобная модель назы­вается двухзонной и представляет собой уточнение модели с сосредоточенными параметрам