2014-02-04
13992
Преобразования называются эквивалентными, если при замене одного участка цепи другим, более простым, токи и напряжения участка цепи, который не был преобразован, не изменяются.
При расчете электрических схем часто возникает целесообразность преобразования схем этих цепей в более простые и удобные для расчета.
Одним из основных видов преобразования электрических схем, применяемых на практике, является преобразование схемы со смешанным соединением элементов. Смешанное соединение элементов представляет собой сочетание более простых соединений – последовательного и параллельного.
Последовательное соединение элементов цепи – соединение нескольких элементов, через которые проходит один и тот же ток.
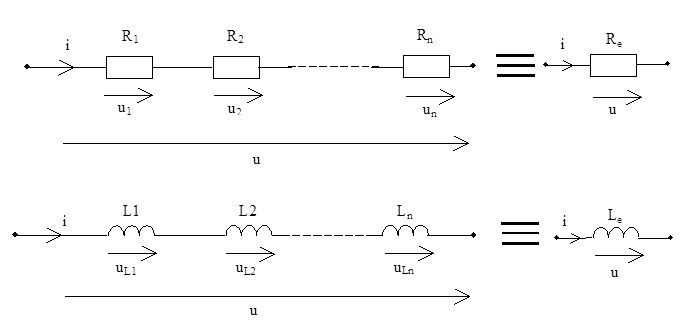
Рисунок 3.1 Схемы последовательного соединения резисторов и индуктивностей
В соответствии с принципом эквивалентного преобразования и законом Ома имеем:
; 
. 
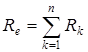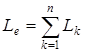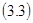
Параллельное соединение элементов
Параллельное соединение элементов – соединение нескольких элементов, при котором все эти элементы находятся под одним и тем же напряжением.
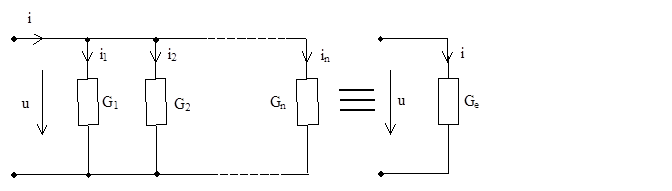
Рисунок 3. 2 Схема параллельного соединения сопротивлений
Имеем:
; 
. 
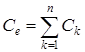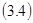
Рассмотрим параллельное соединение двух сопротивлений. В соответствии с 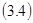для участка цепи с 
, 
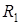(на вышеприведенном рисунке),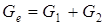 
. Поскольку
, 
, 
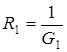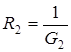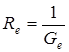, то:
.
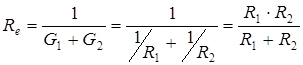Найдем ток в каждой из параллельных ветвей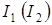 
, если известен общий ток 
и значения сопротивлений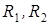 
. По закону Ома 
; 
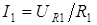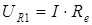. Тогда:
.
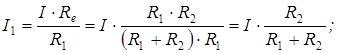
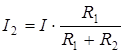Полученное выражение является формулой распределения токов: ток в одной из параллельных ветвей равен общему току, умноженному на сопротивление противоположной ветви и поделенному на сумму сопротивлений обеих ветвей.
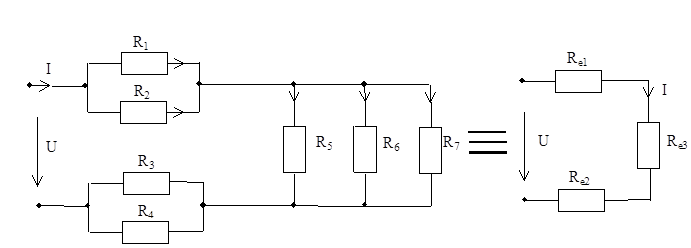
Рисунок 3.3 Схема параллельно-последовательного соединения сопротивлений
Эквивалентное преобразование треугольника сопротивлений в звезду и обратно.
Если известны сопротивления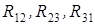 
, которые образуют между узлами 
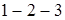треугольник сопротивлений, то для расчета сопротивлений 
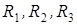, которые соединены в эквивалентную звезду между теми же самыми узлами, используют формулы:
; 
; 
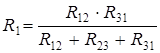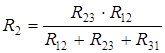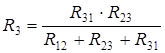. (3.5)
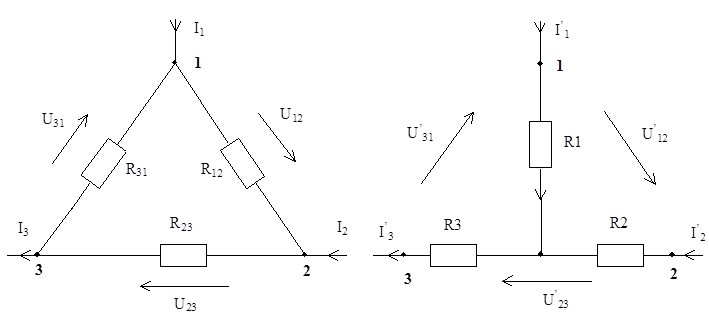
а) б)
Рисунок 3.4 Схемы соединения сопротивлений треугольником (а) и звездой (б)
Обратное преобразование осуществляется при помощи формул:
; 
; 
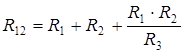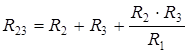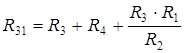(3.6)
Эквивалентные преобразования схем с источниками.
Закон Ома для участка цепи с источником.
Рассмотрим понятие одноконтурной и двухузловой схем.
Эти схемы характерны тем, что имеют один контур (рисунок 3.5) и один независимый контур (рисунок 3.6) соответственно.
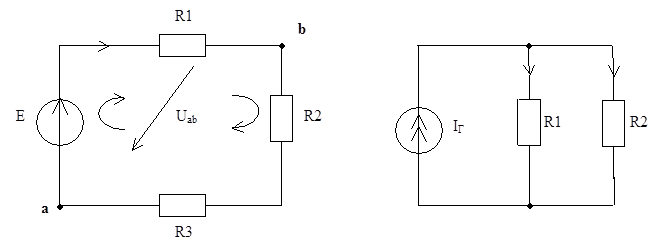
Рисунок 3.5 Одноконтурная схема Рисунок 3.6 Двухузловая схема
Найдем ток в первой схеме. Обозначим напряжение между точкам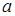и 
и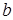 
: 
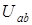. Тогда для двух условных контуров получим два уравнения:
; 
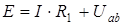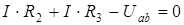
Из первого уравнения получаем закон Ома для участка цепи с источником напряжения:
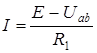
Реальные источники электрической энергии и их эквивалентные схемы.
Реальный источник напряжения – активный элемент, который можно представить в виде идеального источника напряжения и последовательно соединенного с ним пассивного элемента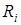 
, (внутреннего сопротивления), которое учитывает потери энергии в источнике (рисунок 3.7).
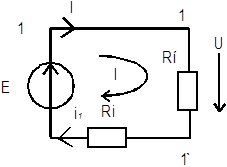
Рисунок 3.7 Схема реального источника напряжения
По закону Кирхгофа можно записать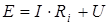 
, откуда получаем выражение для вольт - амперной характеристики реального источника напряжения: 
.
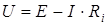Штриховой линией показана ВАХ идеального источника напряжения: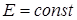 
.
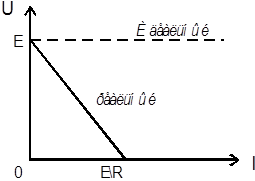
Рисунок 3.8 Вольт-амперная характеристика реального источника напряжения
Выясним, при каких условиях реальный источник приближается к идеальному. Найдем напряжение на зажимах реального источника, к которому подключается сопротивление нагрузки (рисунок 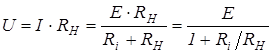3.7)
(3.7)
Из уравнения 3.7 видно, что источник напряжения можно рассматривать как идеальный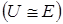 
, если выполняется условие 
.
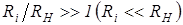Реальный источник тока – активный двухполюсник, который состоит из идеального источника тока и параллельного включенного с ним пассивного элемента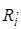 
, который учитывает потери (рисунок 3.9).
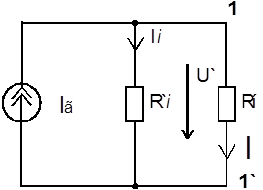
Рисунок 3.9 Схема реального источника тока
В соответствии с первым законом Кирхгофа можно записать:
.
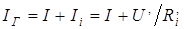Это выражение описывает ВАХ реального источника тока (рисунок 3.10). Штриховой линией показана ВАХ идеального источника тока:
.
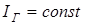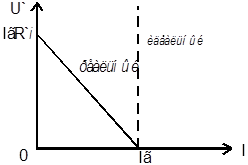
Рисунок 3.10 Вольт-амперная характеристика реального источника тока
Найдем ток в сопротивлении нагрузки, которая подключена к реальному источнику тока (рисунок). По формуле разложения токов
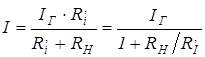. (3.8)
Исходя из формулы (3.8), реальный источник тока приближается к идеальному при условии Ri >> RH.
Некоторые схемы реальных источников напряжения (рисунок 3.7) и тока (рисунок 3.9) эквивалентны. Выясним, при каких условиях? В соответствии с принципом эквивалентных преобразований, напряжение во внешней цепи (т.е. на опорной нагрузке) не может измениться при переходе от схемы (рисунок 3.7) к схеме (рисунок 3.9): U = U`.
Для первой схемы:
,
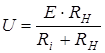Для второй:
,
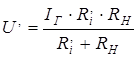если U=U`, то
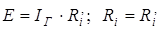. (3.9)
Итак, схемы реальных источников напряжения и тока эквивалентны, если выполняются условия (3.9).
После изучения подразделов 3.1 и 3.2 дайте письменные ответы на контрольные вопросы, приведенные ниже.
