2014-02-02
626
Дифференциальные уравнения и передаточные функции
Рассмотрим обобщенную структурную схему САР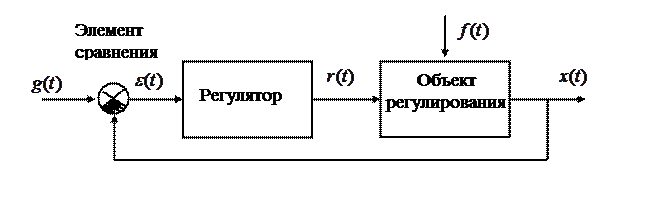 
Пусть элементы САР характеризуются следующими диф. уравнениями, записанными в операторной форме:
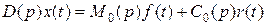- объект регулирования;
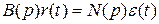- регулятор;
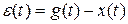- элемент сравнения.
Используя обозначения:
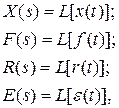
Преобразуем эти уравнения по Лапласу при нулевых начальных условиях:
;
;
.
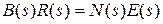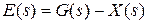Введем следующие обозначения:
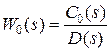- передаточная функция объекта регулирования;
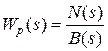- передаточная функция регулятора;
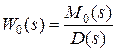- передаточная функция объекта регулирования по возмущению.
Получим следующую структурную схему:
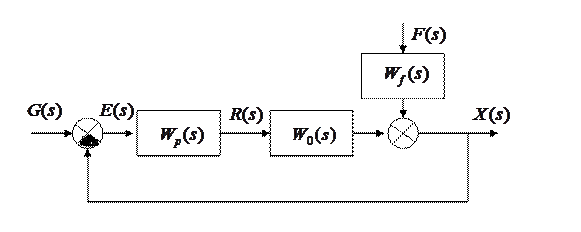
В соответствии со структурной схемой найдем изображение регулируемой величины
.
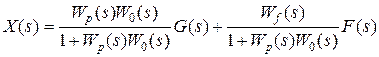Обозначим:
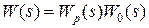, тогда
.
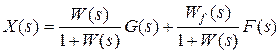Аналогично определяется изображение ошибки:
.
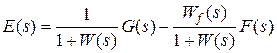Используя обозначения
,
,
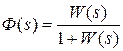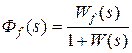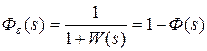, получим
;
.
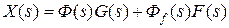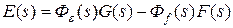Выясним, что представляют собой функции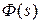 
, 
, 
, 
, 
.
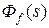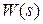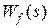Пусть к системе не приложено возмущающее воздействие, т. е. F(s)=0.
Имеем
;
.
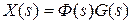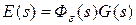Откуда найдем
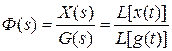- передаточная функция замкнутой САР по управляющему воздействию.
|
|
|
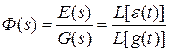- передаточная функция замкнутой САР по ошибке.
Теперь пусть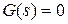 
, т. е. к системе не приложено управляющее воздействие. Получим
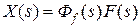, откуда
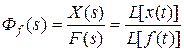- передаточная функция замкнутой САР по возмущающему воздействию.
Для выявления смысла 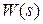и 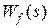разорвем в САР обратную связь. В этом случае сигнал с выхода системы не поступает ее вход. Поэтому входным сигналом для регулятора будет служить не 
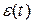, а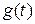 
. Получим
.
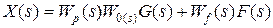Полагая F(s)=0, получим
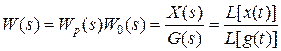- передаточная функция САР в разомкнутом состоянии по управляющему воздействию.
Полагая G(s)=0, получим
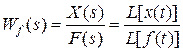- передаточная функция САР в разомкнутом состоянии по возмущению.
Если в рассмотренных выше передаточных функциях положить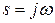 
, то получим соответствующие амплитудно-фазовые частотные характеристики системы. С их помощью могут быть рассмотрены многие стороны работы САР.
Отметим здесь некоторые свойства передаточных функций САР.
Пусть на вход системы поступает
.
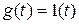Реакция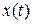 
на это воздействие есть переходная функция
.
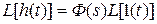Т.к.
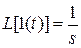, то будем иметь
.
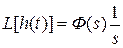Используя теорему о начальном значении, найдем
.
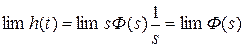Таким образом, начальное значение переходной функции равно конечному значению передаточной функции, при s стремящемся к бесконечности.
Используя теорему о предельном значении, найдем
.
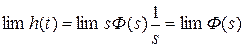Следовательно, конечное значение переходной функции равно начальному значению передаточной функции, при s стремящемся к нулю.
