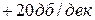Интегрирующими называются звенья, работа которых описывается диф. уравнением вида
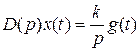 .
.
В них имеет место в установившемся режиме линейная зависимость между входной величиной и производной выходной величины или другими словами выходная величина пропорциональна интегралу по времени от входной величины.
а) Идеальное интегрирующее звено.
Диф. уравнение
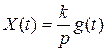
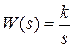
Временные характеристики определяются:
- переходная функция 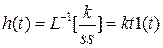
- весовая функция 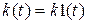
Амплитудно-фазовая характеристика 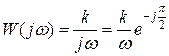

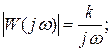
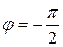
ЛАЧХ
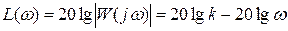 - прямая линия.
- прямая линия.
Если 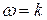 , то
, то 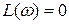 ;
;
если 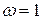 , то
, то 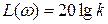
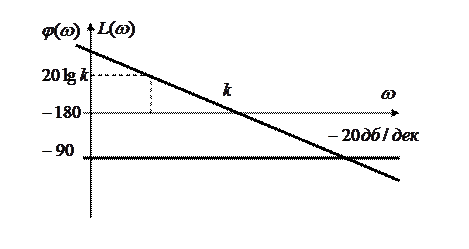
б) Интерпретирующее звено с замедлением (реальное инт. звено) описывается уравнением 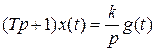
Передаточная функция  может рассматриваться как последовательное соединение идеального интегрирующего и апериодического звеньев.
может рассматриваться как последовательное соединение идеального интегрирующего и апериодического звеньев.
в) Изодромное звено.
Описывается диф. уравнением 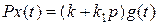 .
.
Передаточная функция 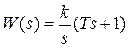 , где
, где 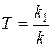 может рассматриваться как параллельное соединение интегрирующего и пропорционального звеньев
может рассматриваться как параллельное соединение интегрирующего и пропорционального звеньев 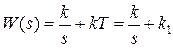 .
.
3. Дифференцирующие звенья – называются такие, у которых в установившемся режиме выходная величина пропорциональна производной по времени от входной.
|
|
|
а) Идеальное дифференцирующее звено.
Диф. уравнение 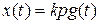
Передаточная функция 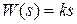
Переходная функция 

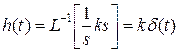
Весовая функция 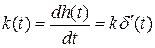 .
.
Амплитудно-фазовая характеристика 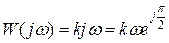
АЧХ 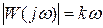
АФХ 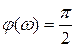
ЛАЧХ 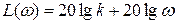 - прямая линия.
- прямая линия.
|
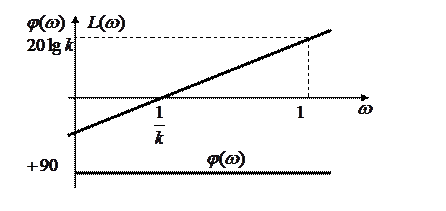
Если 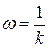
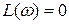 ; если
; если 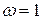
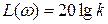 .
.
б) Дифференцирующее звено с замедлением описывается диф. уравнением 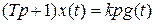
Передаточная функция 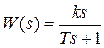 может рассматриваться как последовательное соединение идеального дифференцирующего и апериодического звеньев
может рассматриваться как последовательное соединение идеального дифференцирующего и апериодического звеньев 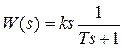 .
.
 2014-02-02
2014-02-02 2219
2219