Устойчивость линейных систем

Из вышеизложенного следует, что об устойчивости системы можно судить по общему решению однородного диф. уравнения

D(P)X=0, (1)

определяющему переходной процесс системы. Чтобы исследовать устойчивость САР, оказывается, нет необходимости находить решение, так как оно зависит от вида корней характеристического уравнения САР.

D(s)=0 или a₀sⁿ+a₁s^n-1+...+a_n=0 (2)

Пусть корни этого уравнения s_i i=1..n. Они могут быть либо вещественными, либо комплексно-сопряженными. Для вещественных корней s_i =a_i, для комплексно-сопряженных корней s_i,t+1 =a±jb. Вещественные корни будем считать частным случаем комплексных при b_i =0. Тогда для устойчивости линейного уравнения n-го порядка с постоянными коэффициентами необходимо и достаточно, чтобы корни характеристического уравнения имели неположительные вещественные части. При исследовании САР особый интерес представляет случай асимптотической устойчивости. Для этого необходимо и достаточно, чтобы вещественные части корней характеристического уравнения были отрицательны, то есть Re s_i <0.Иными словами, все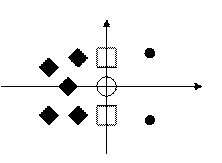корни характеристического уравнения САР должны располагаться в левой полуплоскости на плоскости корней.

Если хотя бы один вещественный или пара мнимых корней находятся на мнимой оси (a_i=0), а все остальные корни расположены в левой полуплоскости, считается, что САУ находится на границе устойчивости. Различают апериодическую и колебательную границы устойчивости. Система находится на апериодической границе устойчивости, если в характеристическом уравнении (2) имеется хотя бы один нулевой корень. На плоскости корней располагается вначале координат (0). Один нулевой корень может появиться в (2) если a_n=0. Тогда (1) может быть представлена в виде

(a₀p^n-1+a₁p^n-2+...+a_n-1)px=0

Таким образом, система оказывается устойчивой не относительно регулируемой величины, а относительно скорости ее изменения dx/dt=px. Сама же регулируемая величина может принимать произвольные значения. Система к ней безразлична, поэтому такие системы часто называют нейтрально устойчивыми.

Система находится на колебательной границе устойчивости, если в характеристическом уравнении (2) имеется хотя бы одна пара чисто мнимых корней. В системе при этом устанавливаются незатухающие гармонические колебания.

Прямой путь определения устойчивости системы состоит в отыскании корней характеристического уравнения, однако он весьма трудоемок, особенно при n³3. Поэтому очень важно знать признаки, по которым можно судить об устойчивости САУ без непосредственного определения корней. Эти признаки называются критериями устойчивости.

Простейшим необходимым (но недостаточным) является критерий, согласно которому необходимо, чтобы все коэффициенты характеристического уравнения (2) были одного знака, например, положительными. Для доказательства представим характеристический полином в виде

D(s) = a₀(s-s₁)(s-s₂)...(s-s_n)

В асимптотически устойчивой системе, все корни имеют отрицательные вещественные части.

Пусть, например s₁= -a₁ s_2,3= -a₂±jb₂... s_n= -a_n.

Тогда

D(s)= a₀(s+a₁)(s+a₂-jb₂)(s+a₂+jb₂)...(s+a_n)=

= a₀(s+a₁)(s²+2a₂ s +2a₂²+b₂²)...(s+a_n)

Откуда следует, что характеристический полином устойчивой САР может быть представлен в виде произведений многочленов 1-ой и 2-ой степени с положительными коэффициентами. При перемножении этих многочленов получается многочлен имеющий только положительные коэфициенты. Нетрудно видеть, что для систем, описываемых диф уравнениями первого и второго порядка, необходимый критерий устойчивости одновременно является и достаточным.