II
Пусть 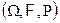 —вероятностное пространство, а
—вероятностное пространство, а 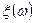 — случайная величина на нем. Функцией распределения случайной величины
— случайная величина на нем. Функцией распределения случайной величины 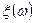 называют функцию
называют функцию
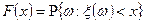 .
.
Свойства функции распределения 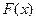
1) Если 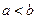 , то
, то 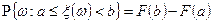 .
.
2) Если 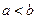 , то
, то 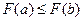 , т.е.
, т.е. 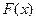 — неубывающая функция.
— неубывающая функция.
3) а)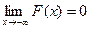 ; б)
; б)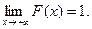
4) 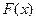 непрерывна слева, т.е.
непрерывна слева, т.е. 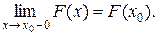
5) 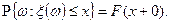
6) 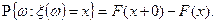
Доказательство.
1) Если 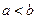 , то
, то 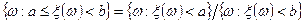 , причем
, причем 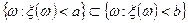 , отсюда и из свойств вероятностей следует требуемое.
, отсюда и из свойств вероятностей следует требуемое.
2) Если 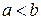 , то
, то 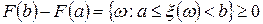 .
.
3) Покажем, что для любых последовательностей 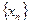 и
и 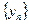 таких, что
таких, что
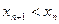 ,
, 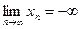 ,
, 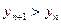 ,
, 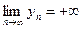 .
.
Имеют место равенства:
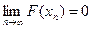 ,
, 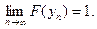
Не трудно увидеть, что:
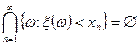 и
и 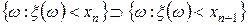 .
.
Поэтому, применяя свойство непрерывности, имеем
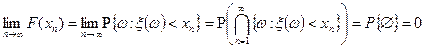 .
.
Далее
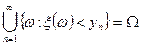 и
и 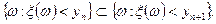
Поэтому, по свойству непрерывности вероятностной меры, получим:
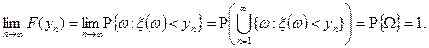
4) Пусть 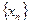 – произвольная числовая последовательность такая, что
– произвольная числовая последовательность такая, что
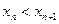 ,
, 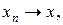
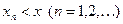 .
.
Покажем, что 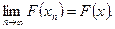
Не трудно видеть, что имеет место равенство:
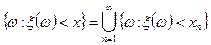 .
.
Так как
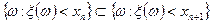 ,
,
то по свойству непрерывности вероятности
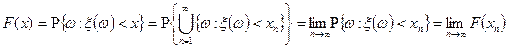 .
.
5) По определению 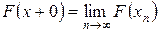 , где
, где 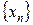 — числовая последовательность такая, что
— числовая последовательность такая, что 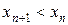 ,
, 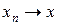 ,
, 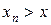 . Поскольку
. Поскольку
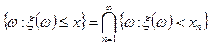 ,
,
а также
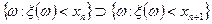 .
.
Согласно свойству непрерывной вероятности
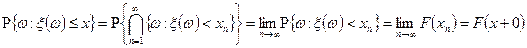 .
.
6) Так как
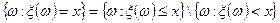 ,
,
а также
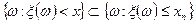 ,
,
то
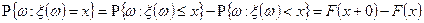 .
.
 2014-02-05
2014-02-05 321
321








