Аксиоматика теории вероятностей

Рассмотрим некоторый стохастический эксперимент. Пусть 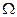— пространство элементарных событий. Предположим, что в 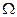выделена система подмножеств 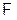, являющаяся 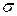–алгеброй. Это означает, что:

S.1) если 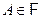, то ;

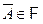
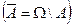S.2) из того, что 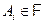, 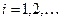следует, что .

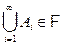Множества из 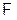называют случайными событиями.

Предположим, что каждому случайному событию 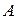(множеству из 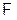) поставлено в соответствие число 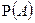(назовем его вероятностью случайного события 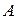), обладающее следующими свойствами:

P.1) 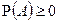для каждого ;

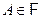P.2) ;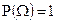

P.3) если 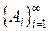, — последовательность случайных событий такая, ч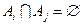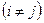то , то .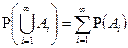

Утверждения S.1, S.2, P.1, P.2, P.3 составляют систему аксиом теории вероятностей. В таком виде аксиоматика теории вероятностей была сформулирована А.Н. Колмогоровым.

2. Определение. Пусть 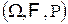— вероятностное пространство. Набор случайных событий 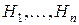, , 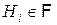, 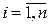образует полную группу событий, если выполнены соотношения

1),

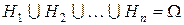2).

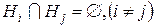Теорема. Формула полной вероятности. Пусть 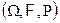— вероятностное пространство. 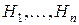, , 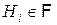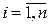— полная группа событий и 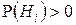, , 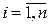то для любого случайного события 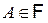имеет место равенство

.

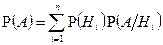Теорема. Формулы Байеса. Пусть 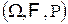— вероятностное пространство. События 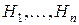, , 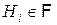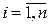образуют полную группу событий, причем 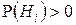, для каждого 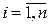. Тогда для любого случайного события 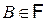такого, что 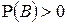, выполнены равенства

.

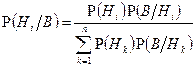3. Определение Пусть 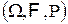— вероятностное пространство. Всякая действительная функция 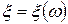на 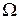такая, что для каждого действительного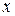 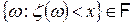, называется случайной величиной.

Определение Функция 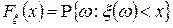называется функцией распределения случайной величины .

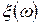Определение Величины 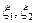называются независимыми, если для любых действительных 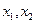события 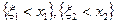независимы, т.е.

.

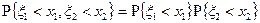4. Определение. Пусть 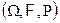— вероятностное пространство. Случайная величина 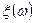называется дискретной случайной величиной, если она принимает конечное или счетное число значений.