1) Если 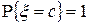 , то
, то 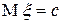 .
.
2) 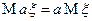 .
.
3) Если  и
и 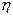 имеют математическое ожидание, то имеет место формула
имеют математическое ожидание, то имеет место формула 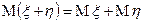 .
.
4) Если 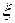 и
и 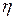 независимы и имеют математическое ожидание, то
независимы и имеют математическое ожидание, то
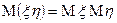
Доказательство. Первое свойство очевидно. При доказательстве второго и третьего остановимся на случае дискретных случайных величин. Пусть случайные величины 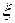 и
и 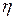 имеют соответственно ряды распределения
имеют соответственно ряды распределения
| 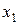
| 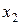
| … | 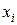
| … | 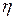
| 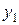
| 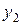
| … | 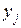
| … | ||
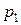
| 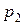
| … | 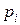
| … | 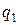
| 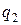
| … | 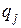
| … |
тогда случайная величина 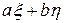 представима в виде (не все числа верхней строки различны!)
представима в виде (не все числа верхней строки различны!)
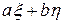
| 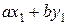
| … | 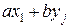
| … | 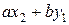
| … | 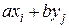
| … |
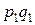
| … | 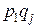
| … | 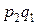
| … | 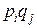
| … |
C учетом соотношений
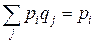 и
и 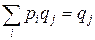 ,
,
Получим, что
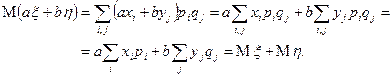
Пусть случайные величины  и
и 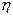 такие, что
такие, что 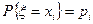 ,
, 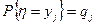 . Тогда
. Тогда
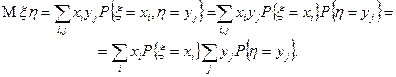
 2014-02-05
2014-02-05 322
322








