Пусть  — последовательность независимых случайных величин, для которых существуют
— последовательность независимых случайных величин, для которых существуют  , причем
, причем 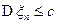 при всех
при всех 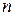 . Тогда
. Тогда
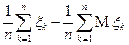
сходится к нулю по вероятности.
Доказательство. Из неравенства Чебышева следует
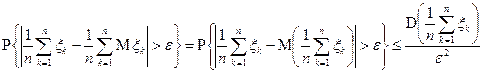 .
.
В силу независимости случайных величин  и ограниченности дисперсий, имеем
и ограниченности дисперсий, имеем
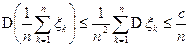 .
.
Таким образом, для всех 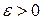 справедливо
справедливо
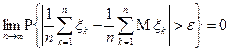 .
.
 2014-02-05
2014-02-05 398
398








