Пусть 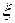 и
и 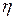 независимые случайные величины с функциями распределения
независимые случайные величины с функциями распределения 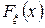 и
и 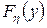 соответственно. Найти функцию распределения
соответственно. Найти функцию распределения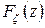 величины
величины 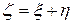 .
.

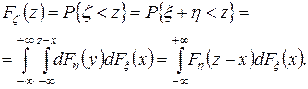
Так как случайные величины входят в сумму симметрично, то, аналогично предыдущим рассуждениям, имеем
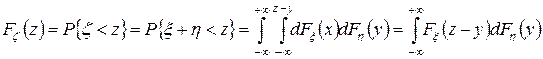 .
.
Таким образом, справедливо
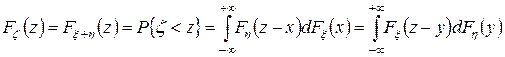 .
.
| Определение | Функция 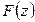 , определяемая формулой , определяемая формулой 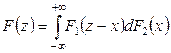 , называетсясверткой функций распределения , называетсясверткой функций распределения 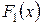 и и 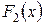 и обозначается и обозначается 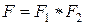 . . |
Если 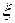 и
и 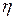 независимы, имеют плотности распределения
независимы, имеют плотности распределения 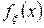 и
и 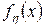 соответственно, то
соответственно, то
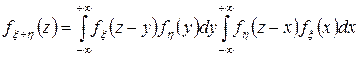 .
.
| Определение | Функция 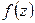 , определяемая формулой , определяемая формулой 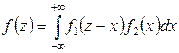 называется сверткой плотностей распределения называется сверткой плотностей распределения 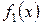 и и 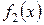 и обозначается и обозначается 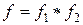 . . |
Если 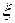 и
и 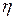 независимые целочисленные дискретные случайные величины такие, что
независимые целочисленные дискретные случайные величины такие, что 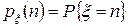 и
и 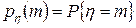 ,
, тогда справедливы формулы
тогда справедливы формулы
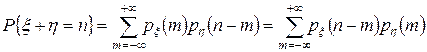 .
.
Пример. Найдем распределение суммы двух независимых случайных величин 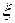 и
и 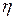 , имеющих распределение Пуассона с параметрами
, имеющих распределение Пуассона с параметрами 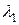 и
и 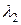 :
:
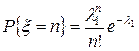 ,
, 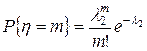 ;
; 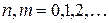
Используя формулу суммы получим
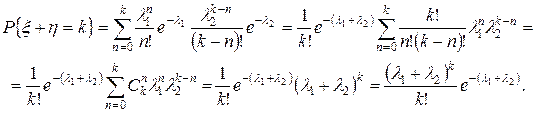
Таким образом, сумма двух независимых случайных величин, имеющих распределение Пуассона с параметрами 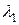 и
и 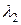 , распределена по закону Пуассона с параметром
, распределена по закону Пуассона с параметром  .
.
 2014-02-05
2014-02-05 9657
9657








