| Теорема. Неравенство Чебышева | Пусть 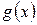 — неотрицательная неубывающая на множестве значений случайной величины — неотрицательная неубывающая на множестве значений случайной величины 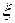 функция. Предположим, что существует функция. Предположим, что существует 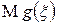 . Тогда для каждого . Тогда для каждого 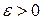 справедливо справедливо
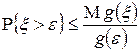 . .
|
Доказательство. Пусть 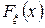 — функция распределения
— функция распределения 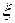 . Применяя формулу (12.1), получим
. Применяя формулу (12.1), получим
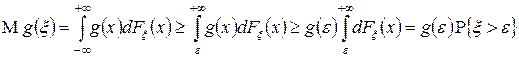 .
.
Что и доказывает теорему
 2014-02-05
2014-02-05 463
463








