Теорема Маркова

Обобщение закона больших чисел для зависимых случайных величин было получено А.А. Марковым.

Теорема. Если последовательность произвольных случайных величин 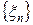удовлетворяет условию

,

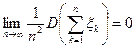тогда для любого 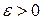имеет место

.

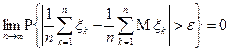Доказательство. Рассмотрим случайную величину 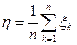, ее числовые характеристики равны 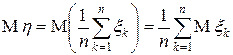и 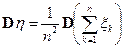. Следовательно, на основании неравенства Чебышева имеем

.

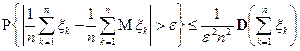Откуда и следует утверждение теоремы.