Лекція № 3. Задача коммивояжера
На контейнерную площадку под выгрузку прибыли вагон (вагоны) с контейнерами. Каждый контейнер (2, 3, 4, 5) должен быть выгружен в соответствующую секцию (6, 7, 8, 9).
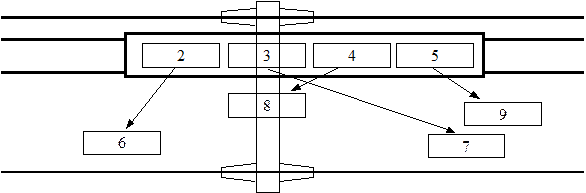
Продолжительности пробегов крана приведены в табл. 1. Найти оптимальную очередность выгрузки, обеспечивающую минимальную продолжительность грузовых операций, если в начальный момент кран находится в состоянии 1.
| от \ до | ||||||||
| 0,5 | 0,5 | - | - | - | - | |||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | 2,3 | - | |
| - | - | - | - | - | - | - | 2,5 | |
| - | 5,2 | 6,5 | - | - | - | - | ||
| 6,6 | - | - | - | - | - | |||
| 2,5 | - | 3,5 | - | - | - | - | ||
| 6,5 | 5,9 | 5,6 | - | - | - | - | - |
Ввиду того, что продолжительность операций выгрузки контейнеров одинакова для всех вариантов, то достаточно оптимизировать направление возврата крана за очередным контейнером после выгрузки предыдущего. В этом случае матрица прбегов будет выглядеть следующим образом.
| До От | (2®6) | (3®7) | (4®8) | (5®9) | |
| - | 5,5 | 2,8 | 3,5 | ||
| - | 11,2 | 8,3 | |||
| 11,6 | - | 7,3 | 6,5 | ||
| 7,5 | - | 6,0 | |||
| 11,5 | 11,9 | 7,9 | - |
Задача коммивояжера решается методом ветвей и границ. При этом перед очередной итерацией определяется верхняя граница решения В - т.е. лучшее решение которое мы знаем на данный момент. Выполняется направленный перебор вариантов на каждом шаге которого определяется нижняя граница решения Н - т.е. наименьшее возможное значение показателя при принятом на данном шаге порядке обхода вершин. Если на каком-то шаге нижняя граница превысит верхнюю, то от дальнейший перебор вариантов в данном прекращается и выполняется анализ альтернативных решений. Если получено допустимое решение, то изменяется верхняя граница и выполняется анализ альтернативных решений.
1) Составить произвольный план, например (1,6) (6,7) (7,8) (8,9) (9,1). Продолжительность возвратов крана а контейнерами составит 5,5+11,2+7,3+6,0+0=30. Полученный результат представляет собой верхнюю границу В=30.
2) Выполнить редукцию строк и столбцов матрицы. Для этого в каждой строке определяем минимальный элемент и вычитаем его со всех элементов строки. После этого та же операция повторяется со столбцами. (В данной таблице редукцию строк не выполняем т.к. каждая из них содержит) 0.
| Ci | Ai | ||||||
| - | |||||||
| - | 5,2 | 5,5 | 5,5 | 5,2 | |||
| 6,1 | - | 4,5 | 3,0 | ||||
| - | 2,5 | 2,0 | |||||
| 5,9 | 5,1 | - | 5,1 | ||||
| Qj | 5,5 | 2,8 | 3,5 | 17,8 | |||
| Bj | 2,0 | 2,0 | 4,5 | 2,0 |
3) Добавить в маршрут одно ребро. Вероятнее всего в граф будет входить ребро, исключение которого максимально увеличит продолжительность выгрузки. Для определения этого ребра необходимо рассчитать штрафы Ai, Bj: в каждом строке найти нулевой элемент и определить ему альтернативу (т.е. минимальный элемент за исключением данного); эта же процедура повторяется и для столбцов.
Определяем значение нижней границы Н=5,5+6+2,8+3,5=17,8. Таким образом, продолжительность выгрузки не может быть меньше 17,8 мин. На дереве поиска рисуем вершину, на которой указываем нижнюю и верхнюю границы.
Определяем дополнительный пробег, вызываемый исключением ребра ij:
Ф ij = Ai + Bj
| Ф16=0+2=2 Ф17=0+2=2 Ф18=0+4,5=4,5 Ф19=0+2=2 | Ф61= 5,2+0=5,2 Ф71=3+0=3 Ф81=2+0=2 Ф91=5,1+0=5,1 |
При исключении этого ребра нижняя граница составляет 17,8+5,2=23
Чтобы определить нижнюю границу решения в которое входит ребро 9.8 из матрицы необходимо исключить соответствующие строку и столбец.
| Ci | |||||
| - | |||||
| 6,1 | - | 4,5 | |||
| - | 2,5 | ||||
| 5,9 | 5,1 | - | 5,1 |
| Ci | Ai | |||||
| - | ||||||
| 3,1 | - | 1,5 | 1,5 | |||
| - | 0,5 | |||||
| 0,9 | 0,8 | - | 5,1 | 0,8 | ||
| Qj | 10,1 | |||||
| Bj | 0,9 |
Нижняя граница решения составляет 17,8+10,1=27,9
| Ф19=0+0=0 Ф17=0+0=0 Ф18=0+0=0 | Ф79=1,5+0= 1,5 Ф86=0,9+0=0,9 Ф87=0+0=0 Ф98=0,8+0=0,8 |
| Ci | Ai | ||||
| - | |||||
| - | |||||
| 0,9 | - | 0,9 | |||
| Qj | |||||
| Bj | 0,9 |
| Ф17=0+0=0 Ф18=0+0=0 | Ф86=0+0=0 Ф87=0+0=0 Ф98=0+0,9=0,9 |
| - | ||
| - |
В результате получено новое решение 1-7-9-8-6-1. Продолжительность выгрузки составляет 27,9 мин.
Далее необходимо рассмотреть только ветвление ВСЕ - т.к. нижние границы остальных ветвлений выше новой верхней границы.
| Ci | ||||||
| - | ||||||
| - | - | 5,2 | 5,5 | 5,5 | 5,2 | |
| 6,1 | - | 4,5 | ||||
| - | 2,5 | |||||
| 5,9 | 5,1 | - |
| Ci | Ai | ||||||
| - | |||||||
| - | - | 0,3 | 5,2 | ||||
| 6,1 | - | 4,5 | |||||
| - | 2,5 | ||||||
| 5,9 | 5,1 | - | 5,1 | ||||
| Qj | 5,2 | ||||||
| Bj | 0,3 |
| Ф16=0+2=2 Ф17=0+0=0 Ф18=0+0=0 Ф19=0+0=0 | Ф67=0+0=0 Ф69=0+0=0 Ф71=3+0=3 Ф91=5,1+0= 5,1 |
| Ci | |||||
| - | |||||
| - | 0,3 | ||||
| 6,1 | - | 4,5 | |||
| - | 2,5 |
| Ci | |||||
| - | |||||
| - | 0,3 | ||||
| 3,1 | - | 1,5 | |||
| - | 0,5 | ||||
| Qj |
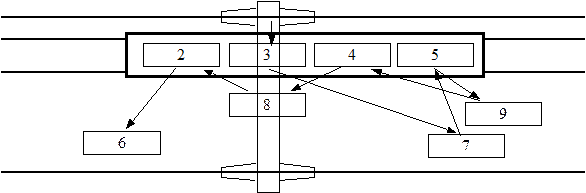
Новая нижняя граница составляет 23+5=28, что больше верхней границы решения. Таким образом, лучшим порядком выгрузки контейнеров является следующий:
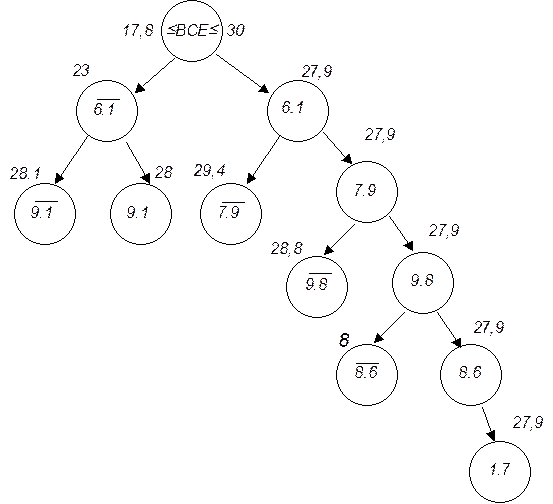
ДВНЗ «ПДАБА»
 2014-02-02
2014-02-02 377
377







