Подсасывающая сила

Дополнения к теореме о подъемной силе.

В исходном виде теорема Жуковского еще непригодна для количест­венных оценок силы, так как нужно ещё определить вели­чину циркуляции. Этой цели служит постулат Жуковского — Чаплы­гина: острая задняя кромка профиля обтекается плавно, и скорость потока на ней имеет конечное значение.

С математической точки зрения этот постулат дает необходимое дополнительное условие для определения циркуляции. С физиче­ской точки зрения он отражает свойства течений вязкой жидкости. В самом деле, если бы точка схода струй располагалась не на ост­рой задней кромке, а где-либо на верхней или нижней поверхности профиля (рис. 5.3), то тогда существовало бы обтекание острой задней кромки, что привело бы к возникновению бесконечно боль­ших отрицательных давлений. Для реальной жидкости это приводило бы к отрыву потока. Значит, условие плавного схода струй с острой задней кромки есть условие безотрывного обтекания задней кромки профиля.

Приведенной теории можно придать более конкретный физиче­ский смысл. Логично допустить, что при плавном сходе струй с зад­ней кромки, скорости жидкости на верхней и нижней поверхностях должны быть равны между собой. Согласно уравнению Бернулли в этом случае и давления сверху и снизу должны быть равны. Сле­довательно, непосредственно на задней кромке отсутствует перепад давления и несущая способность задней кромки равна нулю.

При обтекании профиля циркуляционным потоком невязкой жидкости возникает поперечная скорости набе­гающего потока сила, а продольная

составляющая — сила сопротивления — отсутствует.

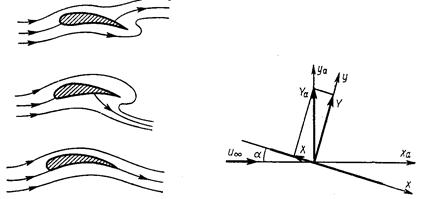
Рис.5.3 Рис.5.4

Такая ситуация на первый взгляд выглядит парадоксальной. В самом деле, предположим, что профиль пред­ставляет собой отрезок прямой линии (пластину). В невязком по­токе существуют только силы давления, которые перпендикулярны поверхности пластины. Поэтому их равнодействующая будет также перпендикулярна к ней. Между тем, согласно теореме Жуков­ского, равнодействующая перпендикулярна скорости набегающего потока (рис. 5.4). Парадокс устраняется, если предположить, что на передней острой кромке возникает разрежение бесконечной ве­личины, так что произведение бесконечного разрежения на беско­нечно малую площадь остается конечным. Сила X, возникающая на передней кромке, является тянущей, обычно ее называют подса­сывающей силой. Проекции сил X и Y на направление набе­гающего потока равны между собой, но противоположны по знакам, так что суммарное сопротивление оказывается равным нулю. В ре­альной жидкости бесконечные разрежения существовать не могут. В окрестности острой кромки поток отрывается, и подсасывающая сила не реализуется. Это приводит к появлению дополнительного сопротивления. Значит, в реальных конструкциях нужно стремиться к обеспечению плавного обтекания передней кромки. Для этой цели применяют профили с плавными обводами носовой части, а в случае необходимости и отклоняемые носики (предкрылки).