Расчет гидродинамических характеристик профиля

Ограничим­ся случаем так называемого «тонкого» профиля, имеющего малые 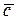и 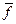. Будем также считать, что профиль обтекается под малым углом атаки. Отсюда можно предположить, что профиль будет вносить в поток малые возмуще­ния, и задачу можно линеаризовать. В линейной постановке задача распадается на две отдельные, независимые друг от друга задачи: задачу о подъемной силе и задачу о толщине. В первом случае рас­сматривается обтекание средней линии (криволинейной дужки) нулевой толщины, во втором — обтекание телесного профиля при нулевой подъемной силе.

Нам нужно решить задачу о подъемной силе. Из условия непроницаемости стенки следует

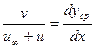
Представим течение в виде суперпозиции равномерного посту­пательного потока со скоростью 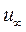и непрерывного распределения вихрей на отрезке оси х от 0 до b с погонной интенсив­ностью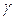

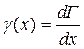(5.1)

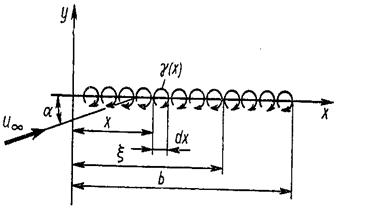
Рис.5.5 Схема профиля крыла.

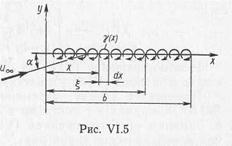Набегающий поток ориен­тирован к хорде профиля под углом атаки 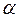(рис. 5.5). Требуется найти зависимость 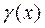, удовлетворяющую гра­ничному условию (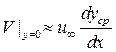) и условию Жуковского Чаплыгина ().

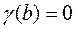Элементарный вихрь интенсивности dГ, расположенный в точке x, индуцирует в точке (ζ, 0) вертикальную скорость

.

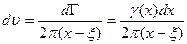Тогда суммарная индуцированная всеми вихрями скорость в точке (ζ,0) будет равна

.

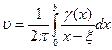Учитывая суммарную скорость в рассматриваемой точке с учетом граничного условия перейдем к интегральному уравнению, решение которого даст нам функцию .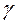

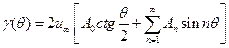(5.2)

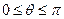
После чего вычислим коэффициент подъемной силы, равный:

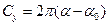, где (5.3)

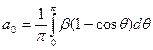— угол атаки нулевой подъемной силы.

Момент тангажа относительно носика:

.

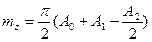С учетом выражения для С_y:

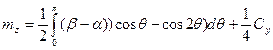
Окончательно получаем

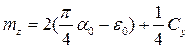, где (5.4)

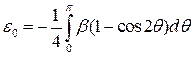
Константы α₀ и ε₀ вычисляются по известному выражению y(x), в котором переменная x заменяется переменной θ по ,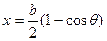

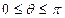
Рас­смотрим неискривленный профиль. Тогда 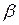=dy_cp/dx=0 и поэтому =0, =0. Следовательно,

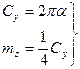(5.5)

Найдем центр давления (точку, где приложена подъемная сила):

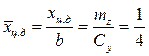(5.6)

Итак, подъемная сила на плоском тонком профиле приложена на расстоянии 1/4 хорды от носика.

Решение задачи можно искать иным путем. Вихревой слой раз­бивается на ряд отрезков-панелей. На каждой панели интенсив­ность вихревого слоя изменяется заданным образом по х, напри­мер по линейному или квадратичному закону. Интеграл тог­да замещается конечной суммой, и задача сводится к решению сис­темы алгебраических уравнений. В предельном случае на панели может располагаться лишь один вихрь. Тогда координата вихря равна ¼ длины панели, считая от начала, а координата контрольной точки, в которой удовлетворяется условие непротекания, равна ¾ длины панели. Правило «одной четверти – трех четвертей», удовлетворяет условию Жуковского-Чаплыгина.