Несущие свойства крыла бесконечного удлинения

ГИДРОДИНАМИЧЕСКИЕ СИЛЫ И МОМЕНТЫ ЦИРКУЛЯЦИОННОГО ТИПА.

Тема 7. ТЕОРИЯ ПОДВОДНОГО КРЫЛА

Вопросы для самопроверки по ТЕМЕ

1. Что вы понимаете под термином «присоединенные массы».
2. Приведите выражения для присоединенных масс. Объясните их физический смысл.
3. Опишите влияние плоскостей симметрии на значения присоединённых масс.
4. Инерционная природа сил и моментов.
5. Приведите пример расчёта присоединённых масс для тела простейшей формы.

(Лекций 4 ч., СРС 4 ч.)

Несущие свойства крыла бесконечного удлинения. Несущие свойства крыла конечного удлинения. Индуктивное сопротивление. Подводное крыло вблизи свободной поверхности. Нелинейные характеристики крыльев малого удлинения при больших углах атаки.

Под несущими свойствами крыла понимают его способность раз­вивать подъемную силу в различных условиях движения.

Геометрия крыла бесконечного удлинения определяется профилем его поперечного сечения. В технике применяются различные профили:

а) сегментные, (рис. 5.1а)

б) симметричные (рис. 5.1б),

в) несимметричные (рис. 5.1в), с острой задней кромкой. Особый тип профилей составляют

г) клиновидные суперкавитирующие (рис. 5.1г).

Типичная конфигурация профиля приведена на рис 5.2. Отрезок прямой, соединяющий две крайние точки профиля, называется хордой. Контур верхней и нижней стороны профиля задается обычно в виде ординат y_b(x) и y_H(x), соответственно отсчитываемых от хорды. Среднее арифметическое этих значений 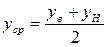дает среднюю линию профиля, называемую иногда скелетной линией.

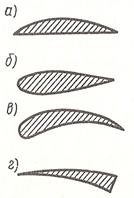
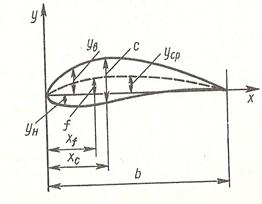
Рис. 5.1 Профили Рис.5.2 Конфигурация профиля

Интегральные характеристики профилей характеризуются глав­ным образом двумя геометрическими параметрами:

1) относитель­ной толщиной 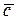=с/b, где с — максимальная толщина профиля,b-хорда и

2) относительным прогибом 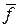=f/b (относительной кривизной), где f — максимальный прогиб средней линии.

Сначала рассмотрим безотрывное сплошное обтекание профиля безграничным потоком жидкости. При этом основной целью явля­ется вычисление подъемной силы. В этих условиях можно остано­виться на модели идеальной жидкости и принять за основу теорему Н.Е.Жуковского.