Влияние вязкости

Учет вязкости вносит коррективы в формулы (5.5), полученные на базе теории идеальной жидкости. В вязкой жидкости коэффициент С_у^а всегда меньше его теоретического зна­чения 2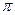.С физической точки зрения проявление вязкости должно происходить через формирование по­граничного слоя и, как следствие, через деформацию истинного контура, включая изменение кривизны вследствие различных ус­ловий течения на верхней и нижней границах. С целью количест­венной оценки поправки на коэффициент подъемной силы, обуслов­ленной вязкостью, поле течения разбивалось на три области: 1) область потенциального потока; 2) область вязкого течения в пограничном слое; 3) область вязкого течения в следе за профилем (рис. 5.6). Течения в каждой области увязывались между собой.

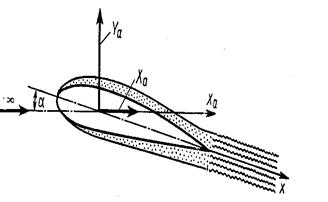
Рис.5.6 Поле течения

В результате проведенных расчетов:

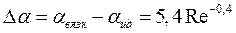(5.7)

Как следует из теоретического решения в рамках идеальной жидкости, на передней кромке наблюдается бесконечный перепад давлений. В реальной же жидкости распределение давле­ния имеет плавный характер (рис.5.7) Важно подчеркнуть, что суммарная подъемная сила формируется как за счет избыточного давления на нижней (нагнетающей) стороне профиля, так и за счет разрежения на верхней (засасывающей) стороне.

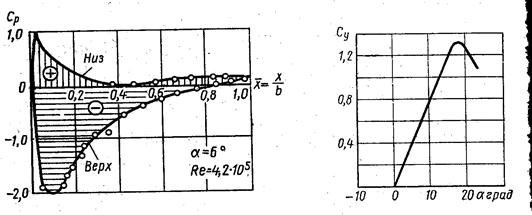
Рис.5.7 Распределение давлений Рис.5.8

Влияние вязкости проявляется также в существовании так на­зываемого критического угла атаки. Линейный закон Су(а) соблюдается лишь до некоторого значения 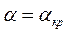, когда С_у достигает значения С_уmах, а затем С_у резко падает (рис. 5.8). Причина падения С_у заключается в срыве пограничного слоя с верх­ней границы профиля под воздействием положительного градиента давления в кормовой зоне.