Операции с матрицами
Квадратная матрица n-го порядка, у которой по диагонали 1, а все остальные элементы 0, называется единичной и обозначается E.
Для любой матрицы A справедливы равенства AE=EA=A. Таким образом, единичная матрица играет роль 1 среди матриц.
Определение 6.1. Матрица B называется обратной к матрице A, если AB=BA=E. Обратная матрица обозначается 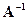 .
.
Понятие обратной матрицы существует только для квадратных матриц.
Свойство 6.1. Если обратная матрица существует, то она единственна.
Доказательство проведем методом от противного. Пусть существует две обратные матрицы к A, которые обозначим через B и C. Рассмотрим произведение BAC. С одной стороны (BA)C=EC=C, а с другой B(AC)=BE=B. Результат не зависит от способа расстановок скобок, поэтому B=C.
Определение 6.2. Матрица называется невырожденной, если ее определитель отличен от 0.
Теорема 6.1. Необходимым и достаточным условием существования обратной матрицы к A является ее невырожденность.
Доказательство. Пусть к матрице A существует обратная 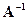 . Из равенства
. Из равенства 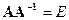 следует равенство определителей
следует равенство определителей 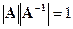 , откуда
, откуда 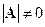 .
.
Пусть 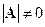 . Построим матрицу B, элементы которой равны
. Построим матрицу B, элементы которой равны 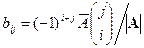 . Найдем AB. Элемент матрицы произведения, стоящий на пересечение строки i и столбца j равен
. Найдем AB. Элемент матрицы произведения, стоящий на пересечение строки i и столбца j равен 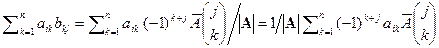 . Сумма
. Сумма 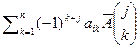 является разложением по строке j определителя матрицы, отличающейся от матрицы A только строкой j, вместо которой стоит строка i. Если
является разложением по строке j определителя матрицы, отличающейся от матрицы A только строкой j, вместо которой стоит строка i. Если 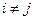 , то эта матрица имеет две одинаковые строки и ее определитель равен 0. Если i=j, то получаем матрицу A. Таким образом, элемент матрицы произведения, расположенный на пересечении строки i и столбца j равен 0 при
, то эта матрица имеет две одинаковые строки и ее определитель равен 0. Если i=j, то получаем матрицу A. Таким образом, элемент матрицы произведения, расположенный на пересечении строки i и столбца j равен 0 при 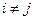 и 1 при i=j, то есть AB=E. Аналогично, проверяется равенство BA=E.Следовательно, матрица B – обратная к A.
и 1 при i=j, то есть AB=E. Аналогично, проверяется равенство BA=E.Следовательно, матрица B – обратная к A.
Следствие 6.1 Если BA=E или AB=E, то  .
.
Доказательство. Если BA=E, то матрица A – невырожденная, и к ней существует единственная обратная матрица. Далее, 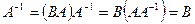 или
или 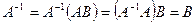 .
.
 2014-02-02
2014-02-02 2023
2023
