Ламинарные и турбулентные течения. Особенностью ламинарного течения является его регулярность. Течение при сохранении ламинарности может изменяться лишь вследствие изменения сил, действующих на жидкость, или внешних условий, в которых она находится. Так, при ламинарном течении в прямолинейной трубе постоянного поперечного сечения частицы жидкости движутся вдоль прямолинейных траекторий, параллельных оси трубы. Однако при достаточно больших скоростях ламинарное течение оказывается неустойчивым и переходит в так называемое турбулентное течение. Турбулентное течение — это такое течение, гидродинамические характеристики которого (скорость, давление, а для газов — плотность и температура) быстро и нерегулярно изменяются во времени (флуктуируют). Частицы жидкости совершают нерегулярные, неустановившиеся движения по сложным траекториям, что приводит к интенсивному перемешиванию между слоями движущейся жидкости. Такие быстрые и нерегулярные изменения происходят не из-за изменений действующих сил или внешних условий, а вследствие неустойчивости ламинарных течений при определенных условиях. Неустойчивость ламинарных течений и возникновение турбулентности — очень сложные вопросы, еще далекие до окончательного решения. Рассмотрение их далеко выходит за рамки нашего курса. Тем не менее имеет смысл привести простейший пример, когда вопрос об устойчивости ламинарного течения решается элементарно.
Парадокс Даламбера. Разрывные течения. Силу, действующую на тело со стороны потока жидкости, можно разложить на две составляющие: в направлении потока Fх и перпендикулярную к потоку Fу. Сила Fx называется лобовым сопротивлением, сила Fy — подъемной силой.
Лобовое сопротивление слагается из двух различных сил: силы разности давлений на переднюю и заднюю поверхности тела и из вязких сил трения. При больших скоростях (точнее, при больших числах Рейнольдса) преобладающую роль играют разности давлений, при малых — силы вязкости.
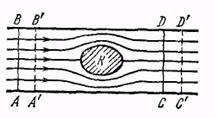
рис.1
2. Рассмотрим, прежде всего, стационарное течение идеальной несжимаемой жидкости. Допустим, что в отсутствие внешних тел жидкость течет параллельным потоком. Поместим в него какое-либо тело К (рис. 1). Оно исказит поток. Но на достаточно больших расстояниях от тела К (в «бесконечности») поток останется параллельным. По истечении некоторого времени движение жидкости установится. К этому установившемуся течению и относятся последующие рассуждения. Для конкретности будем считать, что жидкость течет в прямолинейной трубе. Вдали от тела К линии тока параллельны стенкам трубы и вследствие несжимаемости жидкости скорость ее в этих участках трубы одна и та же. А в силу уравнения Бернулли будет одинаково и давление Р. Рассмотрим часть жидкости ABDC, внутри которой находится тело К. Предполагается, что сечения АВ и CD находятся далеко от тела К, так что через них жидкость течет параллельным потоком. Спустя короткое время выделенная часть жидкости перейдет в положение A'B'D'C'. При этом ее импульс останется без изменения. Следовательно, полная сила, действующая на рассматриваемый объем жидкости в направлении потока, равна нулю. Но эта сила слагается из сил давления на основаниях АВ и CD и из силы F'x, с которой действует на жидкость тело К. (Давление стенок не дает слагающей в направлении потока.) Силы давления на основаниях АВ и CD уравновешивают друг друга, а потому F'x = 0. Следовательно, обращается в нуль и лобовое сопротивление Fx. Допустим теперь, что труба берется все шире и шире. Наш вывод остается справедливым для сколь угодно широкой трубы. Он останется верным и в пределе, когда трубы совсем нет, а поток во всех поперечных направлениях простирается до бесконечности. Итак, при стационарном течении идеальной несжимаемой жидкости или при равномерном движении тела в ней лобовое сопротивление равно нулю. Этот вывод в свое время казался неожиданным. Он получил название парадокса Даламбера (1717—1783). Наличие этого парадокса указывает на то, что при определении лобового сопротивления, испытываемого телом при равномерном движении в жидкости, последнюю нельзя рассматривать как идеальную. Если тело движется неравномерно, то парадокс Даламбера не возникает. Дело в том, что с движущимся телом всегда связана какая-то масса жидкости, увлекаемая им. Она называется присоединенной массой. При ускорении тела ускоряется и присоединенная масса жидкости. Поэтому для сообщения ускорения телу в жидкости требуется большая сила, чем для сообщения такого же ускорения при отсутствии жидкости. Это и значит, что жидкость оказывает сопротивление телу, движущемуся в ней ускоренно.
Этот вывод относится только к лобовому сопротивлению Fx, но не к подъемной силе Fy, и моменту сил М, с которым поток жидкости действует на тело. Момент относительно центра масс равен нулю в тех случаях, когда тело симметрично и симметрично расположено относительно потока. Если такое условие не выполнено, то это, вообще говоря, не так. При обтекании тела происходит смещение всего потока жидкости вбок, т. е. в направлении, перпендикулярном к направлению невозмущенного потока. Это вызывает изменение момента количества движения жидкости и ведет к появлению момента сил, действующего на тело. В результате момент М поворачивает тело, пока он не обратится в нуль и течение жидкости в окрестности тела К вновь станет стационарным.
Парадокс Даламбера легко уяснить, если рассмотреть картину линий тока. На схематическом рис. 265 изображены линии тока при стационарном обтекании цилиндра или шара идеальной жидкостью. Линии тока совершенно симметричны по отношению к направлению вперед и назад (зеркальная симметрия). А скорости частиц жидкости в соответствующих точках перед и за телом равны по величине и отличаются только направлением. Но в уравнение Бернулли скорость входит в квадрате. Поэтому распределения давления в потоке перед и за телом совершенно одинаковы. Давление на переднюю поверхность тела уравновешивается давлением на заднюю поверхность, а следовательно, лобовое сопротивление равно нулю.
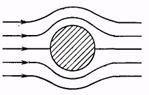
рис.2
Если тело, а следовательно, и поток жидкости не обладают симметрией, то рассуждение усложняется. Однако и в этом случае ввиду отсутствия потерь энергии стационарное течение идеальной жидкости обладает следующим свойством. Пусть пространство MCDN (рис. 3), ограниченное этой перегородкой, заполнено неподвижной жидкостью, находящейся под постоянным давлением Р0. Пусть эту систему тел обтекает идеальная несжимаемая жидкость. Тогда при стационарном течении граница MCDN будет вести себя как поверхность твердого тела, и часть линий тока расположится вдоль этой поверхности. Ширина бесконечно тонких трубок тока в окрестности поверхности MCDN будет изменяться по такому закону, чтобы обеспечить постоянство скорости жидкости вдоль всей поверхности MCDN. Тогда, согласно уравнению Бернулли, будет постоянно и давление жидкости на этой поверхности. Если убрать эластичную перегородку, то характер течения жидкости не изменится. Действительно, поверхность MCDN останется поверхностью постоянного нормального давления, а тангенциальные силы появиться не могут из-за идеальности жидкости. Получилось стационарное течение жидкости с тангенциальным разрывом на поверхности. Оно характеризуется тем, что на некоторой линии обтекаемого тела происходит отрыв течения от тела. Таких течений, очевидно, можно представить бесконечное множество. Они отличаются друг от друга положением линии отрыва CD и формой поверхности тангенциального разрыва MCDN. Давление в области застоя (т. е, области, где жидкость покоится) Р0 равно давлению на линии отрыва CD. Последнее же меньше давления в критической точке В. Это приводит к тому, что равнодействующая сил давления, действующих на переднюю поверхность тела, превышает соответствующую силу, действующую на заднюю сторону его. В результате появляется лобовое сопротивление Fx..
Тангенциальные разрывы гидродинамически неустойчивы. Поверхности разрыва распадаются в вихри.
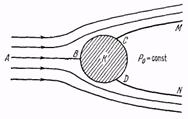
рис.3
Во всем изложенном предполагалось, что поток жидкости является непрерывным. Однако уравнения гидродинамики допускают и такие стационарные течения, в которых скорость жидкости претерпевает разрыв непрерывности.
Таким образом, все движения жидкостей подразделяются на потенциальные и вихревые. Рассмотрим поле скоростей жидкости v (r) в какой-то фиксированный момент времени. Возьмем в жидкости произвольный замкнутый контур С и на нем установим положительное направление обхода (рис. 4). Пусть t — единичный вектор касательной, a ds — элемент длины контура, проведенные в положительном направлении.
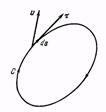
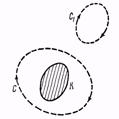
рис.4
Интеграл
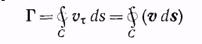
называется циркуляцией вектора скорости по контуру С. Если циркуляция скорости по любому замкнутому контуру обращается в нуль, то движение жидкости называется потенциальным. В противном случае движение называется вихревым.
При этом предполагается, что область пространства, в которой течет жидкость, односвязна. Это значит, что любой замкнутый контур в такой области непрерывной деформацией может быть стянут в точку, не пересекая при этом обтекаемые тела. Если же область не односвязна (например, жидкость, обтекающая тор), то приведенные определения необходимо дополнить следующими замечаниями. В качестве С следует брать не все контуры, а только произвольные замкнутые контуры, которые непрерывной деформацией могут быть стянуты в точку, не выходя при этом за границы жидкости. Важным случаем может служить так называемое плоское течение являющееся идеализацией действительных течений. Пусть обтекаемое тело является бесконечно длинным цилиндром с произвольным поперечным сечением, а жидкость течет перпендикулярно к оси этого цилиндра. Тогда достаточно ограничиться рассмотрением течения в одной из плоскостей, перпендикулярных к той же оси. Течение в этой плоскости и называется плоским. Оно будет потенциальным, если циркуляция скорости обращается в нуль по любому замкнутому контуру, не охватывающему обтекаемый цилиндр, например по контуру С1 (рис. 4). Но циркуляция по контуру С, окружающему цилиндр, может и не обращаться в нуль. При потенциальном течении циркуляция Г будет одной и той же для всех замкнутых контуров, обходящих вокруг цилиндра один раз. Если Г = 0, то говорят о потенциальном течении с циркуляцией.
Определение потенциального течения совершенно аналогично определению консервативных сил. Поэтому при потенциальном течении линейный интеграл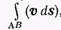 , взятый вдоль незамкнутой кривой, соединяющей точки А и В, зависит только от положения крайних точек этой кривой А и В, но не зависит от формы самой кривой АВ. Рассуждая так же, как в случае потенциальной энергии, можно ввести функцию координат j, через которую скорость выражается формулой
, взятый вдоль незамкнутой кривой, соединяющей точки А и В, зависит только от положения крайних точек этой кривой А и В, но не зависит от формы самой кривой АВ. Рассуждая так же, как в случае потенциальной энергии, можно ввести функцию координат j, через которую скорость выражается формулой 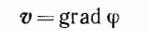
 2014-02-02
2014-02-02 789
789








