Ошибка репрезентативности (ошибка выборки)

Виды выборки

1. Собственно-случайная выборка. Без предварительной подготовки генеральной совокупности случайно или механически из нее извлекают единицы в выборочную совокупность. В данном случае единица отбора совпадает с единицей наблюдения.

2. Стратифицированная типологическая (районированная) выборка. В генеральной совокупности выделяются типы или страты, а затем из каждого типа извлекается число единиц, пропорционально доли каждого типа в общем объеме генеральной совокупности. Единица отбора совпадает с единицей наблюдения.

3. Серийная выборка (гнездовая). В генеральной совокупности выбираются серии (гнезда) и в выборку случайно или механически производят отбор серий. Внутри серий, попавших в выборку, проводится сплошное наблюдение. Чаще всего используется для оценки качества продукции, товаров и в сельском хозяйстве.

4. Многоступенчатая выборка. Связана со сложностью социально-экономических явлений, что не позволяет на первом этапе сформировать окончательно выборочную совокупность. На каждом этапе меняется единица отбора.

5. Многофазная выборка. Каждая фаза отличается объемом программы наблюдения. Чем меньше объем выборки, тем шире программа наблюдения.

Репрезентативная выборка – выборка, которая позволяет получить так называемые несмещенные оценки параметров генеральной совокупности. Выборочную совокупность можно назвать репрезентативной, если распределение единиц в выборке соответствует распределению единиц генеральной совокупности.

При проведении любого наблюдения возникают ошибки наблюдения, которые могут быть случайными и преднамеренными. При достаточно хорошей организации наблюдения этих ошибок можно избежать. При организации выборочного наблюдения возникают ошибки репрезентативности. Эти ошибки связаны не с организацией наблюдения, а с самой сутью выборочного исследования (по части, по выборочной совокупности, приходится судить о целом, о генеральной совокупности). Ошибка выборки неизбежна и состоит в том, что параметры выборочной совокупности (показатели, рассчитанные по выборке) не совпадают с параметрами (показатели генеральной совокупности). Задача исследователя: сформировать выборку, позволяющую получить минимальную ошибку и определить конкретную величину полученной ошибки. Теоретической основой определения ошибки репрезентативности являются теоремы Чебышева, Ляпунова и Бернулли.

Суть теоремы Чебышева: При неограниченном увеличении числа наблюдений в генеральной совокупности с ограниченной дисперсией с вероятностью, близкой к 1, можно утверждать, что величина ошибки выборки не превысит сколь угодно малой положительной величины ε

n → ∞, 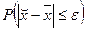→ 1, где

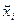- выборочная средняя;

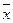- генеральная средняя;

P - вероятность события, заключенного в скобках.

Суть события в том, что ошибка чрезвычайно мала.

Теорема Чебышева доказывает принципиальную возможность оценки параметров генеральной совокупности на основе выборочных данных. Исходя из этой теоремы не ясно, чему равна ошибка выборки и с какой именно вероятностью можно гарантировать непревышение конкретной величины ошибки. На эти вопросы отвечает теорема Ляпунова.

Суть теоремы Ляпунова.

При неограниченном увеличении числа наблюдений в генеральной совокупности с ограниченной дисперсией вероятность того, что ошибка выборки не превысит величины равна нормированной функции Лапласа.

n → ∞, 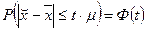, где

μ- средняя ошибка выборки.

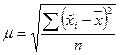, где

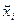- средняя выборочная по i-ой выборке.

n - число выборок.

Данная формула на практике не может быть использована, так как неизвестна величина генеральной средней и фактически проводится всегда лишь одна выборка.

Математической статистикой доказано, что μ² прямо пропорциональна дисперсии генеральной совокупности и обратно пропорциональна объему выборки.

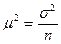, где

σ² – генеральная дисперсия.

Между величинами выборочной и генеральной дисперсий существует зависимость:

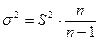, где

S² – выборочная дисперсия.

При большом объеме выборки сомножитель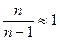

Поэтому на практике его игнорируют и в расчете средней ошибки используют величину выборочной дисперсии.

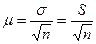
t·μ = Δ - предельная ошибка выборки.

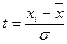- нормированное отклонение

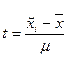- нормированное отклонение выборочной средней от генеральной среденей.

Теорема Ляпунова доказывает, что при большом объеме выборки распределение ошибки выборки подчинено закону нормального распределения.

Для нормального распределения составлены таблицы, в которых зафиксировано отношение t и уровня вероятности.

Задавая уровень вероятности, по таблицам находится соответствующее значение нормированного отклонения. Социально-экономические исследования чаще всего проводятся с вероятностью p = 0.954, t = 1.96 ≈ 2

p = 0.997, t ≈ 3.

Если задана p = 0.954, то Δ = 2·μ

Доверительный интервал:

В условиях большой выборки распределение ошибки выборки подчиняется закону нормального распределения. Поэтому, задавая уровень вероятности, величину t (значение нормированного отклонения) находят по таблице нормированной функции Лапласа.

Выше указанные формулы расчета ошибки выборки разработаны для повторного отбора. В статистике понятие повторного и бесповторного отбора соответствует понятиям возвратного и безвозвратного шара в теории вероятности. Повторный отбор заключается в том, что единица генеральной совокупности, изъятая в выборку, возвращается назад в генеральную совокупность и может быть повторно выбрана в выборочную совокупность. Бесповторный отбор – отобранная из генеральной совокупности единица не возвращается назад.

При повторном отборе на протяжении всего отбора сохраняется неизменная вероятность попадания единицы в выборку p = 1/N

При бесповторном отборе вероятность изменения от 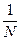для первой единицы отбора до 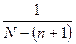для последней единицы отбора.

Поэтому формула средней ошибки выборки для бесповторного отбора, который, как правило, используется в анализе социально-экономических явлений, имеет вид

Величина ошибки выборки зависит также от вида выборки. В формуле средней ошибки при реализации различных видов выборки используются разные дисперсии.