2014-02-02
921
Форма записи линеаризованных
Дифференциальное уравнение записывается таким образом, чтобы выходная величина и все ее производные находились бы в левой части уравнения, а входные воздействия (управляющее воздействие или возмущение) – в правой части. При этом нулевая производная выходной величины (сама величина) должна входить в уравнение с коэффициентом, равным единице. В этом случае исходное дифференциальное уравнение
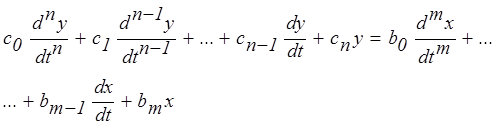
запишется в виде (обе части уравнения поделены на коэффициент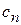 
)
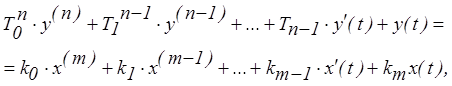
где
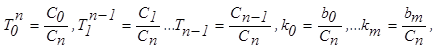
Ti – имеют размерность времени в соответствующей степени и называются постоянными времени, ki – могут иметь различную размерность и называются коэффициентом преобразования (передачи, усиления).
Дифференциальное уравнение часто записывается в операторном виде с использованием алгебраизированного оператора дифференцирования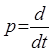 
.
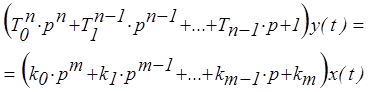Формально из уравнения в операторном виде можно получить выражение для выходной величины (при условном рассмотрении оператора дифференцирования p в качестве алгебраической величины)
или
, 
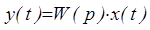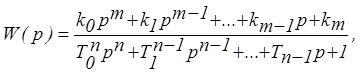
где W(p) – оператор системы (символическая запись дифференциального уравнения системы). В дальнейшем мы уточним значение полученного выражения.
