Проинтегрируем

Время полета ракеты на эллиптической траектории.

Уравнение траектории движения ракеты на эллиптическом участке

Запишем уравнение для момента количества движения точки единичной массы:

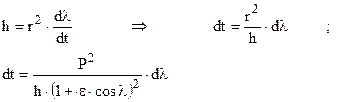
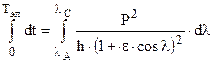
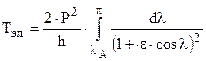- время полета ракеты на эллиптическом участке траектории.

Добавляем “2” и интегрируем до π потому, что берем только половину траектории.

Это уравнение можно решить аналитическим методом или методом численного интегрирования.

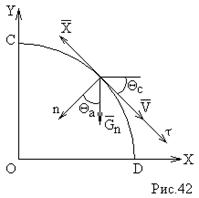
Расчет участка снижения.

Допущения в расчетах:

§ масса спускаемого аппарата постоянна m_СА=сonst;

§ пренебрегаем кривизной Земли и рассматриваем движение в прямоугольных координатах;

§ ускорение свободного падения постоянно g=g_o=const;

§ угол атаки равен нулю α=0, следовательно и подъемная сила равна нулю .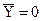

При расчете пассивного участка траектории мы должны получить дальность полета, время, коэффициенты перегрузок (продольные).

y_c=y_a – высота

Θ_с=-Θ_а

V_c=V_a

X_c=0 (X_c=X_a+L_эл)

Уравнение движения ракеты будет:

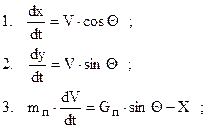
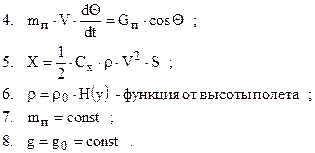
Эта система решается любым численным методом.