.
.
Пусть на отрезке 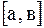 в некоторой последовательности
в некоторой последовательности 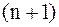 узлов
узлов 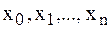 задана функция
задана функция 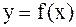 своими значениями
своими значениями 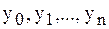 , где
, где 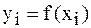 . Задача алгебраического интерполирования состоит в построении многочлена
. Задача алгебраического интерполирования состоит в построении многочлена 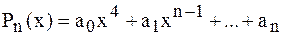 степени
степени 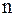 , удовлетворяющего условию интерполирования:
, удовлетворяющего условию интерполирования: 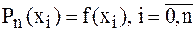 .
.
Известно, что существует единственный полином степени не выше 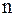 , принимающий в исходных точках заданные значения. Коэффициенты
, принимающий в исходных точках заданные значения. Коэффициенты 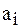 полинома
полинома  можно определить из системы уравнений:
можно определить из системы уравнений:
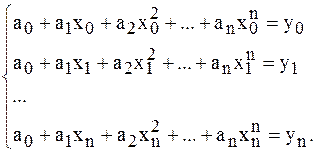
Определитель этой системы есть определитель Вандермонда, и, следовательно, система имеет единственное решение.
Пример. Построить интерполяционный многочлен 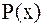 , совпадающий с функцией
, совпадающий с функцией 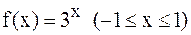 в точках
в точках 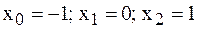 .
.
Решение. Пусть 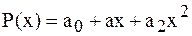 , поэтому имеем
, поэтому имеем
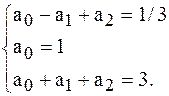 .
.
Отсюда 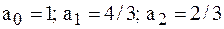 .
.
Поэтому 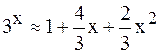 при
при 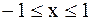 .
.
 2014-02-02
2014-02-02 960
960








