Линейная зависимость функций. Определитель Вронского

Функции 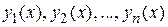называются линейно независимыми в области G, если линейная комбинация этих функций равна нулю

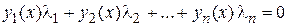
при любом значении 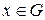только при нулевом наборе чисел

.

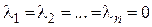В противном случае эти функции называются линейно зависимыми.

Для определения линейной зависимости функций используется определитель Вронского, который имеет вид

.

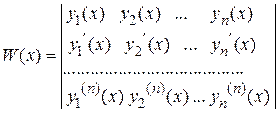Теорема 7.3. Решения линейного однородного дифференциального уравнения 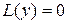являются линейно зависимыми в некоторой области G, если для любого значения x из этой области (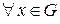) определитель Вронского тождественно равен нулю 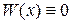, и, наоборот, решения уравнения 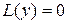линейно независимые, если .

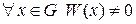Например, покажем, что функци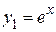и и 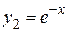являющиеся решениями дифференциального уравнения 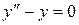, являются линейно независимые. Найдем для этих функций определитель Вронского

.

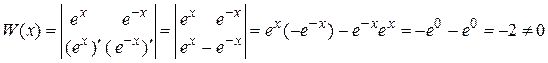Определитель отличен от нуля. Следовательно, функции линейно независимые.