дифференциального уравнения n -ого порядка
Линейному неоднородному дифференциальному уравнению n -ого порядка
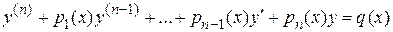
соответствует однородное дифференциальное уравнение
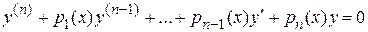 .
.
Пусть линейно независимые функции 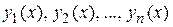 являются решениями линейного однородного дифференциального уравнения
являются решениями линейного однородного дифференциального уравнения 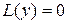 .
.
Покажем, что 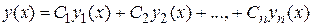 , где
, где 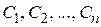 - произвольно заданные постоянные, является общим решением этого уравнения. Для этого необходимо убедиться в том, что при любых начальных условиях можно выбрать произвольные постоянные
- произвольно заданные постоянные, является общим решением этого уравнения. Для этого необходимо убедиться в том, что при любых начальных условиях можно выбрать произвольные постоянные 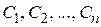 так, чтобы функция
так, чтобы функция 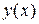 была частным решением дифференциального уравнения с этими начальными условиями.
была частным решением дифференциального уравнения с этими начальными условиями.
Пусть начальные условия имеют вид
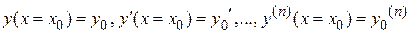 .
.
Составим систему уравнений для нахождения произвольных постоянных 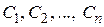 .
.
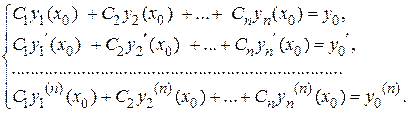
Эта система является системой линейных алгебраических уравнений.
Определитель данной системы представляет собой определитель Вронского
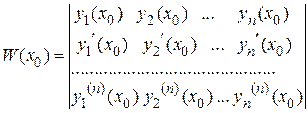 .
.
Этот определитель отличен от нуля, так как функции  линейно независимые. Решение системы (набор значений произвольных постоянных
линейно независимые. Решение системы (набор значений произвольных постоянных 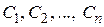 ) можно получить с помощью формул Крамера. Система имеет единственное решение.
) можно получить с помощью формул Крамера. Система имеет единственное решение.
Следовательно, общее решение линейного однородного дифференциального уравнения n -го порядка можно найти как линейную комбинацию n линейно независимых его частных решений.
Таким образом, справедлива следующая теорема.
Теорема 7.4. Общее решение линейного неоднородного дифференциального уравнения n -ого порядка 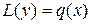 равняется сумме общего решения соответствующего однородного уравнения
равняется сумме общего решения соответствующего однородного уравнения 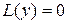 и частного решения этого неоднородного уравнения, т. е.
и частного решения этого неоднородного уравнения, т. е.
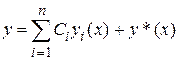 ,
,
где 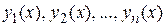 - линейно независимые решения однородного уравнения
- линейно независимые решения однородного уравнения 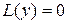 ,
,
 - частное решение неоднородного уравнения
- частное решение неоднородного уравнения 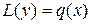 .
.
 2014-02-02
2014-02-02 1870
1870
