Для нахождения решения часто встречающихся в практических исследованиях дифференциальных уравнений n -го порядка с постоянными коэффициентами необходимо рассмотреть комплексные числа и действия над ними.
Комплексным числом называется выражение вида
 ,
,
где  - реальная часть z (действительное число),
- реальная часть z (действительное число),
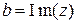 - мнимая часть z,
- мнимая часть z,
 - мнимая единица.
- мнимая единица.
Два комплексных числа 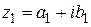 и
и 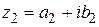 равны, если
равны, если 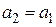 ,
, 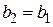 .
.
Комплексное число равно нулю, если 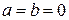 .
.
Два числа  и
и 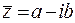 называются комплексно-сопряженными.
называются комплексно-сопряженными.
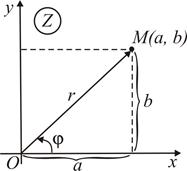 Рис. 83 Рис. 83 | Любое комплексное число  можно изобразить на так называемой комплексной плоскости в прямоугольной декартовой системе координат в виде точки можно изобразить на так называемой комплексной плоскости в прямоугольной декартовой системе координат в виде точки 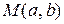 или вектора или вектора 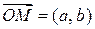 (рис. 83). Длина вектора (рис. 83). Длина вектора 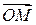 называется модулем комплексного числа называется модулем комплексного числа  и обозначается и обозначается 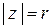 . Очевидно . Очевидно 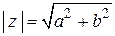 . Обозначим через . Обозначим через 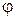 угол, образуемый вектором угол, образуемый вектором 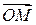 с осью О x. с осью О x. |
Тогда можно записать
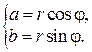 или
или 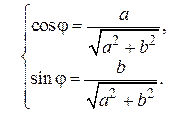
Угол 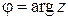 называется аргументом комплексного числа. Аргумент определяется неоднозначно, а с точностью до слагаемого
называется аргументом комплексного числа. Аргумент определяется неоднозначно, а с точностью до слагаемого 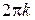 . Сопряженные комплексные числа
. Сопряженные комплексные числа 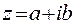 и
и 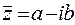 имеют равные модули
имеют равные модули  , а
, а 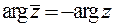 . Любое комплексное число можно записать в тригонометрическом виде
. Любое комплексное число можно записать в тригонометрическом виде 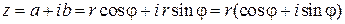 , т. е.
, т. е.
 .
.
Данный вид записи позволяет облегчить действия над комплексными числами.
 2014-02-02
2014-02-02 890
890








