Величина 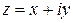 называется комплексной переменной, если x, y – действительные переменные, а
называется комплексной переменной, если x, y – действительные переменные, а  .
.
Комплексная переменная w называется функцией комплексной переменной z с областью определения D и множеством значений Е, если для любого z, принадлежащего множеству D соответствует единственное значение w, принадлежащее множеству Е.
Записывают 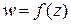 или
или 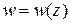 .
.
Функция 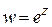 или
или 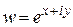 называется показательной функцией комплексной переменной.
называется показательной функцией комплексной переменной.
По определению показательной функции с комплексным показателем
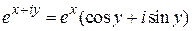 .
.
Например,
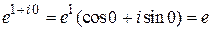 ,
,
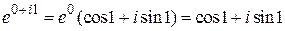 ,
, 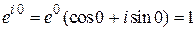 ,
,
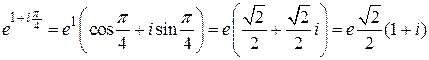 .
.
Показательная функция комплексного переменного обладает всеми теми же свойствами, что и показательная функция действительного переменного.
Покажем, например, что при умножении показательных функций их показатели складываются. Найдем
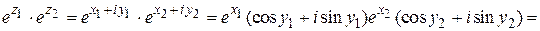
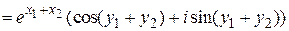 .
.
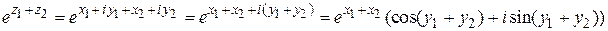 .
.
Следовательно 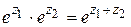 .
.
Аналогично можно показать следующее:
1)  ; 2)
; 2) 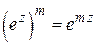 , где m Î Z; 3)
, где m Î Z; 3) 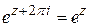 .
.
Комплексная величина
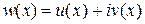 ,
,
где 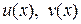 - действительные функции действительной переменной х, называется комплексной функцией действительной переменной.
- действительные функции действительной переменной х, называется комплексной функцией действительной переменной.
Если существуют производные 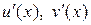 , то выражение
, то выражение

называется производной комплексной функции действительной переменной.
Найдем производную показательной функции 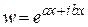 , где a и b – действительные числа. Эту функцию можно записать в виде
, где a и b – действительные числа. Эту функцию можно записать в виде
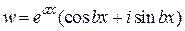 ,
,
т. е. она является комплексной функцией действительной переменной.
Найдем производную этой функции
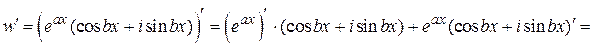
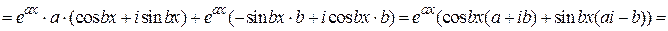
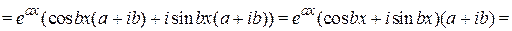
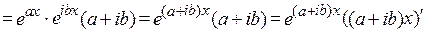 .
.
Следовательно,
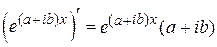 .
.
 2014-02-02
2014-02-02 1857
1857
