Сетевое планирование и управление

Сетевое планиров ание — это метод планирования работ, операции в которых, как правило, не повторяются (например, разработка но­вых продуктов, строительство зданий, ремонт оборудования, проек­тирование новых работ).

Для проведения сетевого планирования вначале необходимо рас­членить проект на ряд отдельных работ и составить логическую схе­му (сетевой граф).

Работа — это любые действия, трудовые процессы, сопровожда­ющиеся затратами ресурсов или времени и приводящие к определен­ным результатам. На сетевых графах работы обозначаются стрелка­ми. Для указания того, что одна работа не может выполняться раньше другой, вводят фиктивные работы, которые изображаются пунктирными стрелками. Продолжительность фиктивной работы принимается равной нулю.

Событие — это факт окончания всех входящих в него работ. Счи­тается, что оно происходит мгновенно. На сетевом графе события изображаются в виде вершин графа. Ни одна выходящая из данного события работа не может начаться до окончания всех работ, входя­щих в это событие.

С исходного события (которое не имеет предшествующих работ) начинается выполнение проекта. Завершающим событием (которое не имеет последующих работ) заканчивается выполнение проекта.

После построения сетевого графа необходимо оценить продолжи­тельность выполнения каждой работы и выделить работы, которые определяют завершение проекта в целом. Нужно оценить потреб­ность каждой работы в ресурсах и пересмотреть план с учетом обес­печения ресурсами.

Часто сетевой граф называют сетевым графиком.

Правила построения сетевых графиков.

1. Завершающее событие лишь одно.

2. Исходное событие лишь одно.

3. Любые два события должны быть непосредственно связаны не более чем одной работой-стрелкой. Если два события связаны более чем одной работой, рекомендуется ввести дополнительное событие и фиктивную работу:

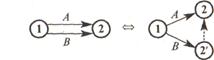
4. В сети не должно быть замкнутых циклов.

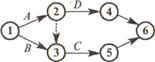
5. Если для выполнения одной из работ необходимо получить ре­зультаты всех работ, входящих в предшествующее для нее событие, а для другой работы достаточно получить результат нескольких из этих работ, то нужно ввести дополнительное событие, отражающее результаты только этих последних работ, и фиктивную работу, свя­зывающую новое событие с прежним.

Например, для начала работы D достаточно окончания рабо­ты А. Для начала же работы С нужно окончание работ А и В.

Метод критического пути

Метод критического пути исполь­зуется для управления проектами с фиксированным временем вы­полнения работ.

Он позволяет ответить на следующие вопросы:

1. Сколько времени потребуется на выполнение всего проекта?

2. В какое время должны начинаться и заканчиваться отдельные
работы?

3. Какие работы являются критическими и должны быть выпол­нены в точно определенное графиком время, чтобы не сорвать уста­новленные сроки выполнения проекта в целом?

4. На какое время можно отложить выполнение некритических работ, чтобы они не повлияли на сроки выполнения проекта?

Самый продолжительный путь сетевого графика от исходного со­бытия к завершающему называется критическим. Все события и рабо­ты критического пути также называются критическими. Продолжи­тельность критического пути и определяет срок выполнения проекта. Критических путей на сетевом графике может быть несколько.

Рассмотрим основные временные параметры сетевых графиков.

Обозначим t (i, j) – продолжительность работы с начальным со­бытием i и конечным событием j.

Ранний срок t_р (j) свершения события j – это самый ранний момент, к которому завершаются все работы, предшествующие этому собы­тию. Правило вычисления:

t_р (j) = max { t_р (i)+ t (j)}

где максимум берется по всем событиям i, непосредственно предше­ствующим событию j (соединены стрелками).

Поздний срок t_n (i) свершения события i – это такой предельный мо­мент, после которого остается ровно столько времени, сколько необ­ходимо для выполнения всех работ, следующих за этим событием.

Правило вычисления:

t_n (i) = min { t_n (j)- t (i, j)}

где минимум берется по всем событиям j, непосредственно следую­щим за событием i.

Резерв R(i) события i показывает, на какой предельно допустимый срок может задержаться свершение события i без нарушения срока наступления завершающего события:

R(i)= t_n (i) – t_р (i)

Критические события резервов не имеют.

При расчетах сетевого графика каждый круг, изображающий событие, делим диаметрами на 4 сектора:

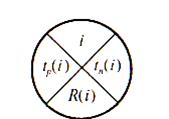
Управление проектами с неопределенным временем выполнения работ

В методе критического пути предполагалось, что время выполне­ния работ нам известно. На практике же эти сроки обычно не опре­делены. Можно строить некоторые предположения о времени вы­полнения каждой работы, но нельзя предусмотреть все возможные трудности или задержки выполнения. Для управления проектами с неопределенным временем выполнения работ наиболее широкое применение получил метод оценки и пересмотра проектов, рассчитанный на исполь­зование вероятностных оценок времени выполнения работ, предус­матриваемых проектом.

Для каждой работы вводят три оценки:

- оптимистическое время а – наименьшее возможное время вы­полнения работы;

- пессимистическое время b – наибольшее возможное время вы­полнения работы;

- наиболее вероятное время т – ожидаемое время выполнения работы в нормальных условиях.

По а, b и т находят ожидаемое время выполнения работы:

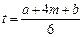
и дисперсию ожидаемой продолжительности t:

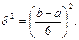
Используя значения t, находят критический путь сетевого графика.

Оптимизация сетевого графика

Стоимость выполнения каждой работы плюс дополнительные расходы определяют стоимость проекта. С помощью дополнитель­ных ресурсов можно добиться сокращения времени выполнения критических работ. Тогда стоимость этих работ возрастет, но общее время выполнения проекта уменьшится, что может привести к сни­жению общей стоимости проекта. Предполагается, что работы можно выполнить либо в стандартные, либо в минимальные сроки, но не в промежутке между ними.

График Ганта

Иногда бывает полезным изобразить наглядно имеющийся в на­личии резерв времени. Для этого используется график Ганта. На нем каждая работа (i, j) изображается горизонтальным отрезком, длина которого в соответствующем масштабе равна времени ее выполне­ния. Начало каждой работы совпадает с ранним сроком свершения ее начального события. График Ганта очень полезен при составлении расписания работ. Он показывает рабочее время, время простоев и относительную загрузку системы. Ожидающие выполнения работы могут быть распределены по другим рабочим центрам.

График Ганта используется для управления работами в процессе. Он указывает, какая работа выполняется по расписанию, а какая опережает его или отстает. Существует много возможностей исполь­зования графика Ганта на практике.

Стоит заметить, что график Ганта не учитывает разнообразия производственных ситуаций (например, поломки или человеческие ошибки, которые требуют повторения работы). График Ганта должен регулярно пересчитываться при появлении новых работ и при пере­смотре продолжительности работ.

График Ганта особенно полезен при работе над проектом с не свя­занными между собой работами. А вот при анализе проекта с тесно взаимосвязанными работами лучше воспользоваться методом кри­тического пути.

Распределение ресурсов, графики ресурсов

До сих пор мы не обращали внимания на ограничения в ресурсах и считали, что все необходимые ресурсы (сырье, оборудование, рабочая сила, денежные средства, производственные площади и т. д.) имеются в достаточном количестве. Рассмотрим один из простейших методов решения проблемы распределения ресурсов – «метод проб и ошибок».

Пример. Произведем оптимизацию сетевого графика по ре­сурсам. Наличный ресурс равен 10 единицам.

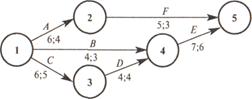
Первое число, приписанное дуге графика, означает время выпол­нения работы, а второе – требуемое количество ресурса для выпол­нения работы. Работы не допускают перерыва в их выполнении.

Находим критический путь. Строим график Ганта. В скобках для каждой работы укажем требуемое количество ресурса. По графику Ганта строим график ресурса. На оси абсцисс мы откладываем время, а на оси ординат – потребности в ресурсах.

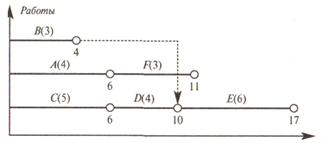
Считаем, что все работы начинаются в наиболее ранний срок их выполнения. Ресурсы складываются по всем работам, выполняемым одновременно. Также проведем ограничительную линию по ресурсу (в нашем примере это у = 10).

Из графика мы видим, что на отрезке от 0 до 4, когда одновремен­но выполняются работы В, А, С, суммарная потребность в ресурсах составляет 3 + 4 + 5 = 12, что превышает ограничение 10. Так как ра­бота С критическая, то мы должны сдвинуть сроки выполнения или А, или В.

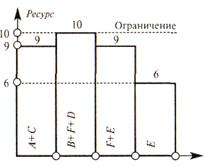
Запланируем выполнение работы В с 6-го по 10-й день. На сроках выполнения всего проекта это не скажется и даст возможность ос­таться в рамках ресурсных ограничений.

Параметры работ

Напомним обозначения: t (i, j) – продолжительность работы (i, j); t_р (i) – ранний срок свершения события i; t_n (i) – поздний срок свер­шения события /.

Если в сетевом графике лишь один критический путь, то его лег­ко отыскать по критическим событиям (событиям с нулевыми резер­вами времени). Ситуация усложняется, если критических путей не­сколько. Ведь через критические события могут проходить как критические, так и некритические пути. В этом случае нужно ис­пользовать критические работы.

Ранний срок начала работы (i, j) совпадает с ранним сроком свер­шения события i: t_pн (i, j) = t_р (i).

Ранний срок окончания работы (i, j) равен сумме t_р (i) и t (i, j): t_pо (i, j) = t_р (i)+ t (i, j).

Поздний срок начала работы (i, j) равен разности t_n (j) (позднего срока свершения события j) и t (i, j): t_пн (i, j) = t_п (j) - t (i, j).

Поздний срок окончания работы (i, j) совпадает с t_n (j): t_по (i, j) = t_п (j).

Полный резерв времени R_n(i, j) работы (i, j) – это максимальный за­пас времени, на которое можно задержать начало работы или увели­чить ее продолжительность, при условии, что весь комплекс работ будет завершен в критический срок:

R_n(i, j)= t_n (j) – t_р (i) – t (i, j)= t_по (i, j) – t_pо (i, j).

Свободный резерв времени R_с(i, j) работы (i, j) – это максимальный запас времени, на которое можно отсрочить или (если она началась в свой ранний срок) увеличить ее продолжительность при условии, что не нарушатся ранние сроки всех последующих работ: R_с(i, j)= t_р (j) – t_р (i) – t (i, j)= t_р (j) – t_pо (i, j).

Критические работы, как и критические события, резервов не имеют.

Пример. Посмотрим, каковы резервы работ для сетевого гра­фика.

Находим t_р (i), t_n (i) и составляем таблицу. Значения первых пяти колонок берем из сетевого графика, а остальные колонки просчитаем по этим данным.

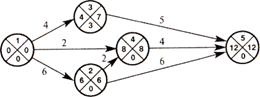
Работа (i, j)	Продолжительность t (i, j)	tр (i)	tр (j)	tn (j)	Срок начала работы
tpн (i, j) = tр (i)	tпн (i, j) = tп (j) - t (i, j)
(1,2)						6-6 = 0
(1,3)						7-4 = 3
(1,4)						8-2 = 6
(2,4)						8-2 = 6
(2,5)						12-6 = 6
(3,5)						12-5 = 7
(4,5)						12-4 = 8

Работа (i, j)	Срок окончания работы	Резервы времени работы
tpо (i, j) = tр (i)+ t (i, j)	tпо (i, j) = tп (j)	Полный Rn(i, j)= = tпо (i, j) – tpо (i, j)	Свободный Rс(i, j)= = tр (j) – tpо (i, j)
(1,2)	0 + 6 = 6		6-6 = 0	6-6 = 0
(1,3)	0 + 4 = 4		7-4 = 3	4-4 = 0
(1,4)	0 + 2 = 2		8-2 = 6	8-2 = 6
(2,4)	6 + 2 = 8		8-8 = 0	8-8 = 0
(2,5)	6 + 6= 12		12-12 = 0	12-12 = 0
(3,5)	4 + 5 = 9		12-9 = 3	12-9 = 3
(4,5)	8 + 4=12		12-12 = 0	12-12 = 0

Критические работы (работы с нулевыми резервами): (1, 2), (2,4), (2, 5), (4, 5). У нас два критических пути: 1 - 2 - 5 и 1 - 2 - 4 - 5.

Методы сетевого планирования и управления позволяют сосре­доточиться на важнейших для выполнения проекта моментах. При этом требуется, чтобы работы были взаимно независимы, то есть в пределах определенной последовательности работ можно начи­нать, приостанавливать, исключать работы, а также выполнять одну работу независимо от другой работы. Все работы должны выполнять­ся в определенной последовательности. Поэтому методы сетевого планирования и управления широко применяются в строительстве, самолетостроении и судостроении, а также в промышленных отрас­лях с быстро меняющимися тенденциями.

Скептическое отношение к методам сетевого планирования и уп­равления часто основывается на их стоимости, которая может со­ставлять около 5% общей стоимости проекта. Но эти расходы обыч­но полностью компенсируются экономией, достигаемой с помощью более точного и гибкого графика, а также сокращения сроков выпол­нения проекта.