5.1 Сила и давление прокатки
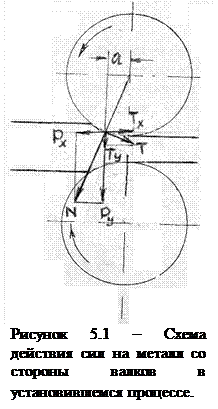
Сила прокатки является одним из важнейших показателей процесса прокатки. Она лежит в основе расчета рабочей клети, передающих устройств, мощности электропривода и пр. По сути, она определяет тип и конструкцию прокатного стана. Под силой прокатки понимают равнодействующую Р всех вертикальных составляющих элементарных сил нормального давления N и сил трения Т, приложенных к металлу со стороны валков (рис. 5.1). горизонтальные составляющие 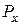 и
и 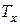 взаимно уравновешивают друг друга, т.е.
взаимно уравновешивают друг друга, т.е. 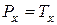 , а вертикальные составляющие Ру и Т у в сумме дают силу прокатки
, а вертикальные составляющие Ру и Т у в сумме дают силу прокатки 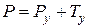 .
.
 Такая же, но противонаправленная сила действует со стороны металла на валки.
Такая же, но противонаправленная сила действует со стороны металла на валки.
При установившемся процессе прокатки равнодействующая сила Р направлена перпендикулярно оси полосы. В противном случае продольная составляющая силы Р вызывала бы либо торможение, либо ускорение полосы.
Сила прокатки 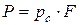 , где рс – среднее нормальное напряжение (давление), которое было бы при условии его равномерного распределения по площади контактной поверхности, F – горизонтальная проекция площади контактной поверхности.
, где рс – среднее нормальное напряжение (давление), которое было бы при условии его равномерного распределения по площади контактной поверхности, F – горизонтальная проекция площади контактной поверхности.
Контактное напряжение зависит от множества факторов, учесть которые чрезвычайно сложно, особенно механические свойства стали.
Поэтому обычно используют или чисто экспериментальные способы, или аналитические, но с учетом экспериментальных значений механических свойств.
Экспериментальным путем измеряют силу прокатки, а уже по ней определяют среднее давление: 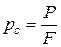 .
.
Точнее, измеряют не собственно силу, а упругие деформации мессдоз или стоек станин клети при прокатке, а уже по ним с использованием тарировочных кривых вычисляют силу прокатки.
Таким путем определяют силу и давление прокатки на действующих станах. Для проектируемых станов используют аналитические методы и эмпирические формулы.
Из эмпирических формул достаточно известна формула Экелунда:
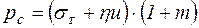 , кг/мм2,
, кг/мм2,
где sТ = (14 - 0,01t) (1,4 + C + Mn + 0,3 Cr). Здесь C, Mn и Cr – содержание этих элементов в стали, %.
h - вязность стали: h = 0,01 (14 – 0,01t)Кv. Здесь Кv – скоростной коэффициент. При V £ 6 м/сек Кv = 1, при V > 6 м/сек Кv = 0,8.
u – скорость деформации.
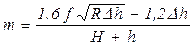 .
.
При аналитическом подходе к решению этой задачи один из возможных способов предложил А.И. Целиков. Контактное напряжение зависит от двух групп факторов.
Первая группа факторов учитывает природные свойства металлов, обычно отождествляемые с пределом текучести sТ. Предел текучести имеет разные значения не только для разных металлов, но и для одного и того же металла в зависимости от температуры прокатки, степени и скорости деформации и пр. Вторая группа - учитывает влияние напряженно-деформированного состояния металла в очаге деформации, выражаемое произведением 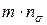 , где m – коэффициент Лоде, учитывает влияние среднего главного напряжения и изменяется в пределах 1,0…1,15, а ns - влияние напряженного состояния металла в очаге деформации. Тогда
, где m – коэффициент Лоде, учитывает влияние среднего главного напряжения и изменяется в пределах 1,0…1,15, а ns - влияние напряженного состояния металла в очаге деформации. Тогда 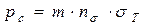 .
.
Проф. В.С. Смирнов, используя положения теории размерностей, предложил определять m по следующим зависимостям: 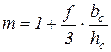 при
при 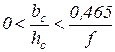 и
и 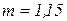 при
при 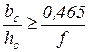 .
.
Второй член 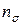 А.И. Целиков представил в следующем виде:
А.И. Целиков представил в следующем виде:
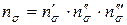 ,
,
где 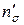 - коэффициент, учитывающий влияние внешнего трения;
- коэффициент, учитывающий влияние внешнего трения;
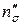 - коэффициент, учитывающий геометрические показатели очага деформации (фактор формы);
- коэффициент, учитывающий геометрические показатели очага деформации (фактор формы);
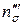 коэффициент, учитывающий влияние натяжения или подпора на давление;
коэффициент, учитывающий влияние натяжения или подпора на давление;
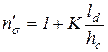 , где К равен
, где К равен 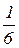 ,
, 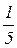 или
или 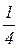 при
при 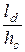 равном до 2, от 2 до 4 и более 4, соответственно.
равном до 2, от 2 до 4 и более 4, соответственно.
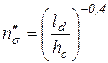 при
при 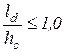 и
и 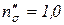 при
при 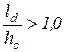 .
.
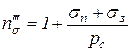 , где
, где 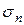 и
и 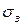 напряжения в переднем и заднем концах полосы, создаваемые натяжением или подпором.
напряжения в переднем и заднем концах полосы, создаваемые натяжением или подпором.
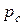 - давление при отсутствии натяжения или подпора.
- давление при отсутствии натяжения или подпора.
При простом случае прокатки 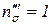 .
.
Третий член 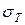 проф. В.И. Зюзин предложил определять с помощью базового сопротивления деформации
проф. В.И. Зюзин предложил определять с помощью базового сопротивления деформации 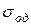 и термомеханических коэффициентов
и термомеханических коэффициентов 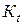 ,
, 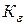 и
и 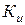 , учитывающих влияние, соответственно, температуры, относительного обжатия и скорости деформации:
, учитывающих влияние, соответственно, температуры, относительного обжатия и скорости деформации: 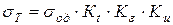 .
.
Базовые значения 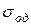 для разных металлов определяют опытным путем при постоянных значениях t = 10000С, e = 10% и
для разных металлов определяют опытным путем при постоянных значениях t = 10000С, e = 10% и 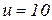 сек-1 и сводят в таблицы.
сек-1 и сводят в таблицы.
Значения термомеханических коэффициентов для разных материалов определяют следующим образом: при фиксированных значениях e = 10% и 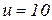 сек-1 определяют сопротивление деформации
сек-1 определяют сопротивление деформации 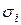 при разных температурах. По полученным значениям коэффициента
при разных температурах. По полученным значениям коэффициента 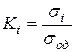 строят график зависимости
строят график зависимости 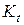 от температуры.
от температуры.
Аналогичным образом определяют значения 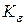 при разных обжатиях и фиксированных значениях t = 10000С и и = 10 сек-1, а также
при разных обжатиях и фиксированных значениях t = 10000С и и = 10 сек-1, а также 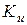 - при разных скоростях деформации при фиксированных значениях t = 10000С и e = 10%.
- при разных скоростях деформации при фиксированных значениях t = 10000С и e = 10%.
При машинных методах расчета удобнее пользоваться не графиками, а следующими функциональными зависимостями для определения термомеханических коэффициентов.
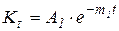 ,
, 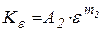 и
и 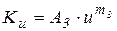 ,
,
где 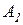 ,
, 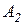 ,
, 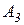 ,
, 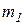 ,
, 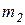 ,
, 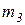 - экспериментальные показатели для разных металлов, е – основание натурального логарифма.
- экспериментальные показатели для разных металлов, е – основание натурального логарифма.
Тогда 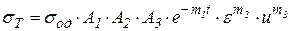 .
.
Таким образом, определив значения m, ns и sТ находят давление прокатки, а по нему - силу прокатки, по которой производят прочностные расчеты рабочей клети, валков, нажимных устройств и пр.
5.2 Момент и мощность прокатки
Момент прокатки можно определять экспериментальным или аналитическим путем.
В первом случае обычно на шпиндели наклеивают проволочные датчики, по упругим деформациям которых и терировочным кривым определяют крутящий момент прокатки на валу приводного двигателя.
Во втором случае момент прокатки МП определяют по найденным значениям сили прокатки.
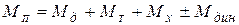 , где
, где
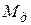 – момент, расходуемый на пластическую деформацию и преодоление контактных сил трения;
– момент, расходуемый на пластическую деформацию и преодоление контактных сил трения;
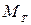 – момент, расходуемый на преодоление сил трения в подшипниках валков, шестеренной клети и пр.;
– момент, расходуемый на преодоление сил трения в подшипниках валков, шестеренной клети и пр.;
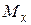 – момент холодного хода, расходуемый на работу главной линии стана в холостом режиме;
– момент холодного хода, расходуемый на работу главной линии стана в холостом режиме;
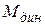 – момент, расходуемый на преодоление инерционных сил в период разгона и торможения двигателя (со знаком + при разгоне, со знаком - при торможении). Учитывается только на реверсивных станах.
– момент, расходуемый на преодоление инерционных сил в период разгона и торможения двигателя (со знаком + при разгоне, со знаком - при торможении). Учитывается только на реверсивных станах.
Момент деформации для двух валков будет 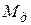 = 2Ра, где а – плечо приложения равнодействующей силы (рис. 5.1). Обычно плечо силы выражают через коэффициент
= 2Ра, где а – плечо приложения равнодействующей силы (рис. 5.1). Обычно плечо силы выражают через коэффициент 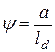 . Тогда
. Тогда 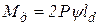 . Коэффициент плеча
. Коэффициент плеча 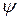 при горячей прокатке изменяется в пределах 0,4…0,6, а при холодной – 0,25…0,35. Для его определения в конкретных условиях прокатки предложены следующие формулы:
при горячей прокатке изменяется в пределах 0,4…0,6, а при холодной – 0,25…0,35. Для его определения в конкретных условиях прокатки предложены следующие формулы:
Формула Чекмарева 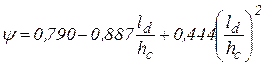 - для горячей прокатки и формула Сафьяна и Мелешко
- для горячей прокатки и формула Сафьяна и Мелешко 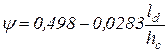 - для холодной.
- для холодной.
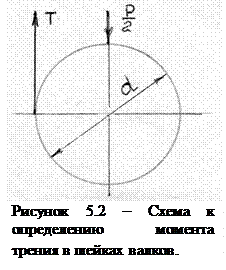 Момент трения в шейках валков
Момент трения в шейках валков 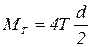 , где d – диаметр шейки рабочих валков (рис. 5.2). Сила трения
, где d – диаметр шейки рабочих валков (рис. 5.2). Сила трения 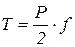 , Тогда
, Тогда 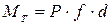 , где f – коэффициент трения в подшипниках.
, где f – коэффициент трения в подшипниках.
Для подшипников скольжения f = 0,01…0,03, для подшипников качения и жидкостного трения f = 0,003.
С учетом потерь на трение в других узлах главной линии стана 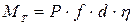 , где
, где 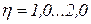 .
.
Момент холостого хода можно принять в пределах 3-5% от суммы моментов Mд и MТ, т.е. Mх = (0,03…0,05)(Mд + MТ).
Динамический момент 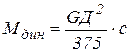 , где GД2 – суммарный маховый момент вращающихся частей главной линии стана;
, где GД2 – суммарный маховый момент вращающихся частей главной линии стана;
с – показатель, характеризующий ускорение или замедление двигателя.
При ускорении с = 30…40 об/мин. сек, при замедлении с = 60…70 об/мин. сек.
Маховый момент 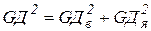 , где
, где 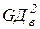 - маховый момент рабочих валков, шпинделей и пр.,
- маховый момент рабочих валков, шпинделей и пр., 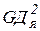 - маховый момент якоря двигателя. Обычно
- маховый момент якоря двигателя. Обычно 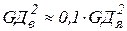 . Тогда
. Тогда 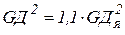 . Значения
. Значения 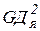 - паспортные данные двигателя.
- паспортные данные двигателя.
Мощность прокатки 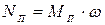 , где
, где 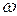 - угловая скорость вращения валков,
- угловая скорость вращения валков, 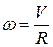 . Тогда
. Тогда 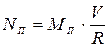 Мнм/сек (мвт).
Мнм/сек (мвт).
Мощность двигателя 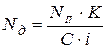 ,
,
где К – скоростной коэффициент, учитывает снижение мощности двигателя вследствие ослабления магнитного потока при частоте вращения валков n выше номинальной nн (паспортные данные): 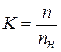 . При n < nн, К = 1,0;
. При n < nн, К = 1,0;
С – коэффициент временной перегрузки двигателя. Для нереверсивных двигателей С = 2,0, для реверсивных С = 2,5…3,0;
i - КПД передачи 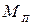 от двигателя к валкам. При наличии шестеренной клети в главной линии стана i = 0,9, при отсутствии - i = 0,95.
от двигателя к валкам. При наличии шестеренной клети в главной линии стана i = 0,9, при отсутствии - i = 0,95.
Мощность приводных двигателей изменяется в широких пределах для разных станов, от нескольких киловатт на лабораторных станах до 6…12 мегаватт на обжимных станах.
 2014-02-02
2014-02-02 7268
7268
