Закон распределения молекул газа по скоростям (закон Максвелла)
В основное уравнение кинетической теории идеального газа входит средняя квадратичная скорость. Смысл ее заключается в том, что это та скорость, которой должны были бы обладать все молекулы (если бы величины их скоростей были одинаковы, а направления равновероятны), чтобы давление газа было таким, каким оно в действительности является.
На самом деле скорости молекул неодинаковы. Благодаря беспорядочным движениям и взаимным столкновениям молекулы газа каким-то образом распределяются по скоростям. Среди них есть и очень быстрые и очень медленные. Теория и опыт показывают, что, несмотря на полную хаотичность движения и случайный характер столкновений, распределение молекул по скоростям оказывается не случайным, не произвольным, а вполне определенным, однозначным и единственно возможным.
Применяя методы теории вероятностей, Максвелл в 1860 г. установил закон распределения молекул идеального газа по скоростям:
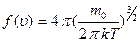
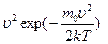 , (2.2.16)
, (2.2.16)
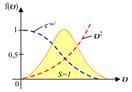 Рис.2.1 Рис.2.1 | где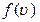 - функция распределения(определяется долей частиц, скорости которых заключены в единичном интервале вблизи скорости - функция распределения(определяется долей частиц, скорости которых заключены в единичном интервале вблизи скорости  ). В показателе экспоненты стоит отношение кинетической энергии молекулы ( ). В показателе экспоненты стоит отношение кинетической энергии молекулы ( ), к величине, характеризующей среднюю энергию молекул газа ( ), к величине, характеризующей среднюю энергию молекул газа (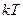 ). ). | ||||
Конкретный вид функции распределения зависит от рода газа (массы 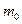 молекулы) и от его температуры молекулы) и от его температуры 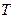 . Давление и объем газа на распределение молекул по скоростям не влияют. Скорость, при которой функция распределения молекул газа по скоростям максимальна, называется наиболее вероятной скоростью . Давление и объем газа на распределение молекул по скоростям не влияют. Скорость, при которой функция распределения молекул газа по скоростям максимальна, называется наиболее вероятной скоростью  . Из закона распределения можно определить некоторые скорости, характерные для данного состояния газа (рис.2.2; табл.2.1). . Из закона распределения можно определить некоторые скорости, характерные для данного состояния газа (рис.2.2; табл.2.1). | 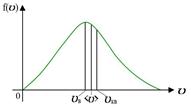 Рис.2.2 Таблица 2.1. Рис.2.2 Таблица 2.1. | ||||
Наиболее вероятная скорость 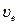 | Средняя арифметическая скорость 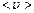 | Средняя квадратичная скорость 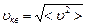 | |||
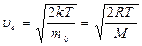 | 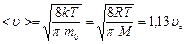 | 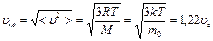 | |||
При появлении в объеме газа неоднородности какой-либо физической величины (плотности газа, температуры или скорости упорядоченного движения его отдельных слоев) возникают потоки вещества, энергии или импульса упорядоченного движения частиц, приводящие к выравниванию пространственного распределения этой физической величины и устранению неоднородности. При этом протекают особые явления, называемые явлениями переноса (они связаны с переносом какой-либо физической величины). К этим явлениям относятся диффузия, теплопроводность и внутреннее трение.
2.4.1. Диффузия - явление самопроизвольного взаимного проникновения и перемешивания частиц двух соприкасающихся газов, жидкостей и даже твердых тел. В химически чистых газах диффузия возникает из-за неоднородности плотности в различных частях объема газа. В смеси газов диффузия вызывается различием в концентрациях отдельных газов в разных частях объема смеси. При постоянной температуре явление диффузии заключается в переносе массы газа из мест, где его концентрация больше в места, где она меньше.
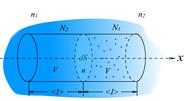 Рис.2.3 Рис.2.3 |
В простейшем одномерном случае диффузиявозникает в химически однородном газе, концентрация n (или плотность 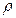 ) которого изменяется вдоль одной координаты
) которого изменяется вдоль одной координаты 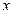 , т. е.
, т. е. 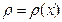 (рис.2.3). Мысленно выделим в газе площадку
(рис.2.3). Мысленно выделим в газе площадку 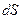 , перпендикулярную оси
, перпендикулярную оси 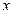 . Молекулы газа проникают через эту площадку в обоих направлениях – слева направо и справа налево. Однако большее число молекул движется с той стороны, где их плотность больше. Поэтому можно говорить о массе газа, перенесенной в определенном направлении. Перенос вещества путем диффузии осуществляется только вдоль оси
. Молекулы газа проникают через эту площадку в обоих направлениях – слева направо и справа налево. Однако большее число молекул движется с той стороны, где их плотность больше. Поэтому можно говорить о массе газа, перенесенной в определенном направлении. Перенос вещества путем диффузии осуществляется только вдоль оси 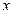 и описывается законом Фика, установленным экспериментально:
и описывается законом Фика, установленным экспериментально:
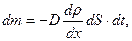 (2.2.17)
(2.2.17)
где  – масса вещества, диффундирующего за время
– масса вещества, диффундирующего за время  через площадку
через площадку 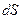 ;
; 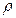 – плотность газа;
– плотность газа;  – градиент (перепад) плотности вдоль оси
– градиент (перепад) плотности вдоль оси 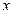 ;
; 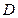 – коэффициент диффузии.
– коэффициент диффузии.
Знак минус в формуле указывает на то, что перенос массы происходит в направлении убывания плотности 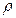 , т. е. вдоль положительного направления оси
, т. е. вдоль положительного направления оси 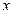 при
при 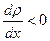 и в обратном направлении при
и в обратном направлении при 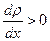 .
.
Из закона Фика следует, что коэффициент диффузии 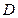 численно равен массе газа, продиффундировавшей за единицу времени через единичную площадку, расположенную нормально к потоку диффузии при градиенте плотности, равном единице.
численно равен массе газа, продиффундировавшей за единицу времени через единичную площадку, расположенную нормально к потоку диффузии при градиенте плотности, равном единице.
Масса вещества, переносимая в единицу времени через единицу площади, т. е. плотность потока массы, 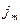 равна
равна 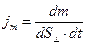 =
= или
или 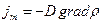 . (2.2.18)
. (2.2.18)
Закон диффузии, выведенный на основании молекулярно-кинетической теории газов, имеет вид: 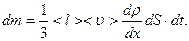 (2.2.19)
(2.2.19)
Сравнив его с законом Фика, получаем, что коэффициент диффузии, равный
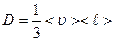 , (2.2.20)
, (2.2.20)
пропорционален средней длине свободного пробега молекул 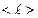 (среднему расстоянию, которое пробегают молекулы от одного столкновения до следующего) и средней арифметической скорости движения частиц
(среднему расстоянию, которое пробегают молекулы от одного столкновения до следующего) и средней арифметической скорости движения частиц  .
.
Единица коэффициента диффузии – 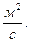
2.4.2. Внутреннее трение (вязкость) возникает между слоями газа или жидкости, перемещающимися параллельно друг другу с различными по модулю скоростями.
Рассмотрим два слоя жидкости (1 и 2), движущихся параллельно друг другу со скоростями 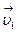 и
и 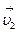 , причем
, причем 
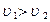 (рис.2.4). Благодаря хаотическому тепловому движению молекулы переходят из слоя в слой и «переносят» импульсы
(рис.2.4). Благодаря хаотическому тепловому движению молекулы переходят из слоя в слой и «переносят» импульсы 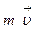 своего упорядоченного движения. При переходе молекул из слоя 1, движущегося быстрее, в слой 2, частицы переносят большие импульсы и соударения между молекулами приводят к ускорению упорядоченного движения слоя 2. При переходе из слоя 2, движущегося медленнее, в слой 1 перешедшие частицы ускоряют свое упорядоченное движение, а молекулы слоя 1 замедляются. В результате этих процессов переноса импульса молекул между слоями 1 и 2
своего упорядоченного движения. При переходе молекул из слоя 1, движущегося быстрее, в слой 2, частицы переносят большие импульсы и соударения между молекулами приводят к ускорению упорядоченного движения слоя 2. При переходе из слоя 2, движущегося медленнее, в слой 1 перешедшие частицы ускоряют свое упорядоченное движение, а молекулы слоя 1 замедляются. В результате этих процессов переноса импульса молекул между слоями 1 и 2
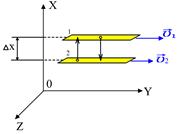 Рис.2.4 Рис.2.4 | возникают силы внутреннего трения, которые определяются законом Ньютона: 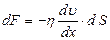 , (2.2.21) где , (2.2.21) где 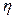 – коэффициент внутреннего трения (динамическая вязкость); – коэффициент внутреннего трения (динамическая вязкость); 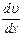 – градиент скорости (показывает, как быстро меняется скорость при переходе от слоя к слою в направлении, перпендикулярном направлению движения слоев); – градиент скорости (показывает, как быстро меняется скорость при переходе от слоя к слою в направлении, перпендикулярном направлению движения слоев); |
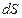 – площадь трущихся слоев. Сила
– площадь трущихся слоев. Сила 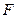 считается положительной, если она ускоряет слой и отрицательной, если тормозит.
считается положительной, если она ускоряет слой и отрицательной, если тормозит.
Закон Ньютона можно записать и для импульса 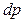 , переносимого частицами при переходах между слоями с различными скоростями направленного движения
, переносимого частицами при переходах между слоями с различными скоростями направленного движения
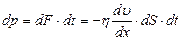 . (2.2.22)
. (2.2.22)
Знак минус указывает на то, что импульс переносится из быстро движущихся слоев в слои, движущиеся медленно. Коэффициент вязкости равен силе внутреннего трения, действующей на единицу поверхности слоя при градиенте скорости равном единице.
На основании кинетической теории можно показать, что сила внутреннего трения равна:
 , (2.2.23)
, (2.2.23)
где <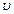 > средняя скорость теплового движения молекул.
> средняя скорость теплового движения молекул.
Из сравнения последней формулы с законом Ньютона, получаем, что коэффициент вязкости, равный 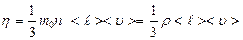 , (2.2.24)
, (2.2.24)
пропорционален средней длине свободного пробега молекул 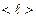 , средней арифметической скорости их движения
, средней арифметической скорости их движения  и плотности газа
и плотности газа 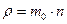 .
.
Единица коэффициента вязкости – пуаз (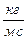 ).
).
2.4.3. Теплопроводность – явление переноса теплоты от слоев газа, обладающих более высокой температурой, и, следовательно, более высоким значением энергии, к слоям с более низкой температурой. Хаотическое тепловое движение молекул приводит к направленному переносу внутренней энергии газа. Молекулы, попавшие из нагретых частей объема газа в более холодные, отдают часть своей энергии окружающим частицам. И наоборот, частицы, движущиеся медленнее, попадая из холодных частей объема газа в более нагретые, увеличивают свою энергию за счет соударений с молекулами, имеющими большие скорости и энергии.
В простейшем одномерном случае явление теплопроводности возникает в газе, температура которого зависит только от одной координаты 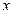 , т. е.
, т. е.  . При этом перенос внутренней энергии газа путем теплообмена осуществляется только вдоль оси
. При этом перенос внутренней энергии газа путем теплообмена осуществляется только вдоль оси 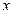 и описывается законом Фурье, установленным экспериментально:
и описывается законом Фурье, установленным экспериментально: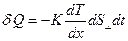 , (2.2.25)
, (2.2.25)
где 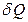 – количество теплоты, которое передается путем теплопроводности за время
– количество теплоты, которое передается путем теплопроводности за время  через площадку
через площадку 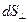 , расположенную перпендикулярно направлению переноса внутренней энергии;
, расположенную перпендикулярно направлению переноса внутренней энергии; 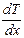 – градиент температуры;
– градиент температуры; 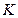 – коэффициент теплопроводности. Знак минус в формуле указывает на то, что перенос внутренней энергии происходит в направлении убывания температуры.
– коэффициент теплопроводности. Знак минус в формуле указывает на то, что перенос внутренней энергии происходит в направлении убывания температуры.
Коэффициент теплопроводности численно равен количеству теплоты, переносимой в единицу времени через единичную площадку, расположенную перпендикулярно направлению теплового потока при градиенте температуры равном единице.
Количество теплоты, переносимое в единицу времени через единицу площади, т. е. плотность теплового потока 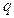 , равна
, равна 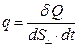 =
=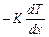 или
или 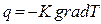 . (2.2.26)
. (2.2.26)
Закон теплопроводности, выведенный с помощью молекулярно-кинетической теории, имеет вид: 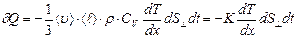 . (2.2.27)
. (2.2.27)
Сравнивая последнюю формулу с законом Фурье, получаем, что коэффициент теплопроводности, равный 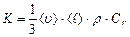 , (2.2.28)
, (2.2.28)
пропорционален средней арифметической скорости  движения частиц, средней длине их свободного пробега молекул
движения частиц, средней длине их свободного пробега молекул 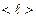 , плотности газа
, плотности газа 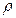 и удельной теплоемкости газа
и удельной теплоемкости газа 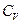 при постоянном объеме.
при постоянном объеме. 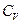 определяет внутреннюю энергию вещества при данной температуре (
определяет внутреннюю энергию вещества при данной температуре (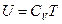 ).
).
В табл. 2.2 приведены уравнения явлений переноса и коэффициентов переноса.
Таблица 2.2
| Явление переноса | Переносимая величина | Уравнение переноса | Коэффициент переноса |
| Диффузия | Масса | Закон Фика 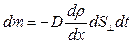 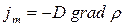 | 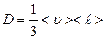 |
| Внутреннее трение (вязкость) | Импульс | Закон Ньютона 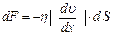 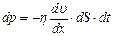 | 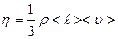 |
| Теплопроводность | Теплота (внутр. энергия) | Закон Фурье 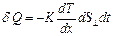 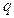 = =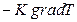 | 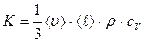 |
Единица коэффициента теплопроводности - 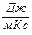 .
.
Внешнее сходство математических выражений всех трех явлений обусловлено одинаковостью механизма перемешивания молекул при их хаотическом движении и столкновениях друг с другом.
Коэффициенты переноса связаны следующими соотношениями:
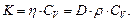 (2.2.29)
(2.2.29)
III. Первое начало термодинамики
Термодинамика не вдается в рассмотрение микроскопической картины рассматриваемых явлений. Она опирается на два основных закона (начала), являющихся обобщением огромного количества данных.
Первое начало устанавливает количественные соотношения при превращениях энергии из одних видов в другие.
 2014-02-02
2014-02-02 2376
2376
