Для равновесных процессов изменения состояния газа первое начало термодинамики 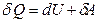 можно записать в виде
можно записать в виде 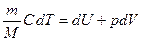 . (2.3.9)
. (2.3.9)
Применим это уравнение к изопроцессам в идеальном газе. Законы изопроцессов получим из уравнения Менделеева-Клапейрона  .
.
Практически изохорный процесс осуществляется при изменении температуры газа, находящегося в толстостенном сосуде постоянного объема. Для такого процесса уравнение состояния идеального газа удобно записать в виде  . Все величины, стоящие в правой части уравнения, постоянные. Следовательно, давление данной массы газа при постоянном объеме возрастает линейно с ростом температуры:
. Все величины, стоящие в правой части уравнения, постоянные. Следовательно, давление данной массы газа при постоянном объеме возрастает линейно с ростом температуры:
 .(2.3.10)
.(2.3.10)
 Рис.3.3 Рис.3.3 | Закон Шарля также описывает линейную зависимость давления газа от температуры. На рис.3.3 изображены  , , 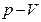 и и 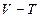 диаграммы изохорного процесса при различных значениях объема диаграммы изохорного процесса при различных значениях объема  газа. Поскольку в данном процессе объем газа не изменяется ( газа. Поскольку в данном процессе объем газа не изменяется (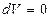 ), то газ работы не совершает ( ), то газ работы не совершает (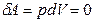 ) и вся сообщаемая теплота идет на изменение его внутренней энергии. Первое начало термодинамики имеет вид: ) и вся сообщаемая теплота идет на изменение его внутренней энергии. Первое начало термодинамики имеет вид: |
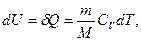 (2.3.11)
(2.3.11)
|
|
|
где 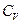 – молярная теплоемкость газа при постоянном объеме (
– молярная теплоемкость газа при постоянном объеме (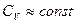 ).
).
При изохорном нагревании газа от температуры  до температуры
до температуры 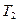 изменение внутренней энергии газа и сообщенная ему теплота равны
изменение внутренней энергии газа и сообщенная ему теплота равны
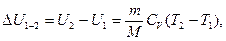
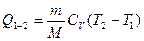 . (2.3.12)
. (2.3.12)
Для любого равновесного процесса первый закон термодинамики можно записать в виде:
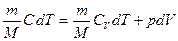 . (2.3.13)
. (2.3.13)
Для 1 моля газа 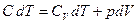 . (2.3.14)
. (2.3.14)
Изобарный процесс ( )
)
Практически изобарный процесс осуществляется, например, при нагревании или охлаждении газа, находящегося в цилиндре с подвижным поршнем, на который действует постоянное внутреннее давление. Для такого процесса уравнение состояния идеального газа удобно записать в виде  . Все величины, стоящие в правой части уравнения, постоянные. Следовательно, объем данной массы газа при постоянном давлении возрастает линейно с ростом температуры:
. Все величины, стоящие в правой части уравнения, постоянные. Следовательно, объем данной массы газа при постоянном давлении возрастает линейно с ростом температуры: 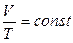 . (2.3.15)
. (2.3.15)
Закон Гей-Люссака также описывает линейную зависимость объема от температуры. На рис.3.4 изображены  ,
,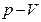 и
и 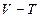 диаграммы изобарного процесса при различных значениях давления
диаграммы изобарного процесса при различных значениях давления 
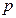 газа.
газа.
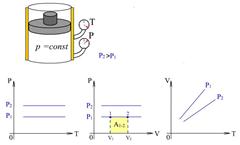 Рис.3.4 Рис.3.4 |
Элементарная теплота 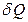 , сообщаемая газу в изобарном процессе, равна
, сообщаемая газу в изобарном процессе, равна
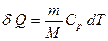 , (2.3.15)
, (2.3.15)
где 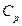 – молярная теплоемкость газа при постоянном давлении, которую также называют изобарной теплоемкостью.
– молярная теплоемкость газа при постоянном давлении, которую также называют изобарной теплоемкостью.
Продифференцируем уравнение состояния газа  при
при  :
: 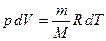 .
.
Следовательно, 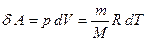 . (2.3.16)
. (2.3.16)
Подставим выражения (2.3.11), (2.3.15) и (2.3.16) в первое начало термодинамики (2.3.3):


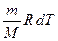 . (2.3.17)
. (2.3.17)
Отсюда следует, что  . (2.3.18)
. (2.3.18)
Это соотношение называется уравнением Майера. Его физический смысл заключается в том, что при изобарном нагревании газа к нему должна быть подведена большая теплота, чем при таком же изохорном нагревании. Разность значений теплоты должна быть равна работе, совершенной газом при изобарном расширении.
|
|
|
Работа, совершаемая газом при изобарном процессе расширения 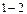
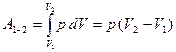
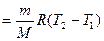 , (2.3.19)
, (2.3.19)
измеряется площадью, закрашенной на 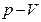 диаграмме.
диаграмме.
Изотермический процесс расширения или сжатия газа может происходить в условиях, когда теплообмен между газом и внешней средой осуществляется при постоянной разности температур. Для этого теплоемкость внешней среды должна быть достаточно велика и процесс расширения (или сжатия) должен происходить весьма медленно.
В уравнении состояния идеального газа  при изотермическом процессе все величины, стоящие в правой части уравнения, постоянные. Следовательно,
при изотермическом процессе все величины, стоящие в правой части уравнения, постоянные. Следовательно,
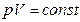 . (2.3.20).
. (2.3.20).
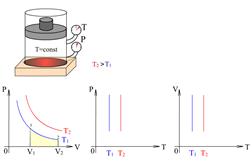 Рис.3.5 Рис.3.5 | Закон Бойля-Мариотта, установленный экспериментально, дает такую же зависимость. На 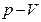 диаграмме (рис.3.5) такой процесс графически изображается изотермой,имеющей вид равнобочной гиперболы. Внутренняя энергия идеального газа в изотермическом процессе ( диаграмме (рис.3.5) такой процесс графически изображается изотермой,имеющей вид равнобочной гиперболы. Внутренняя энергия идеального газа в изотермическом процессе (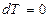 ) не изменяется ) не изменяется 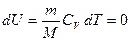 , , |
следовательно, вся теплота, сообщаемая газу, расходуется на совершение газом работы против внешних сил:
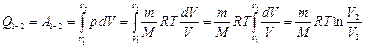 , (2.3.21)
, (2.3.21)
Работа изотермического расширения газа измеряется площадью, закрашенной на 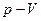 диаграмме.
диаграмме.
Поскольку в данном процессе 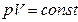 , то
, то  и
и 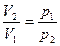 и
и
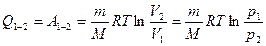 . (2.3.21а)
. (2.3.21а)
Практически адиабатными можно считать процессы быстрого расширения или сжатия газа при которых система не обменивается теплотой с окружающей средой.
Из первого начала термодинамики (2.3.3) для адиабатного процесса (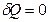 ) получаем, что система совершает работу за счет убыли ее внутренней энергии:
) получаем, что система совершает работу за счет убыли ее внутренней энергии:
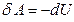 . (2.3.22)
. (2.3.22)
Подставим сюда выражения (2.3.1) и (2.3.11) получим: 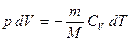 , (2.3.23)
, (2.3.23)
что работа, связанная с изменением объема газа, сопровождается изменением его температуры. Знак «минус» в уравнении означает, что увеличение объема (расширение) сопровождается понижением температуры, а уменьшение объема (сжатие) – повышением.
Уравнение адиабаты или уравнение Пуассона имеет вид:
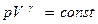 , (2.3.24)
, (2.3.24)
где  – безразмерная величина, называемая показателем адиабаты или коэффициентом Пуассона. Уравнение адиабаты можно записать и через другие параметры
– безразмерная величина, называемая показателем адиабаты или коэффициентом Пуассона. Уравнение адиабаты можно записать и через другие параметры
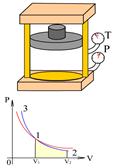 Рис.3.6 Рис.3.6 | состояния: 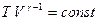 и и 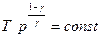 . (2.3.25) Линия, изображающая адиабатный процесс на . (2.3.25) Линия, изображающая адиабатный процесс на 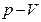 диаграмме (рис.3.6) называется адиабатой (синяя линия). Для сравнения на этом же рисунке красной линией изображена изотерма при температуре газа в состоянии диаграмме (рис.3.6) называется адиабатой (синяя линия). Для сравнения на этом же рисунке красной линией изображена изотерма при температуре газа в состоянии 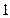 . Так как . Так как 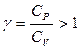 , то адиабата идет круче изотермы. Объясняется это тем, что при адиабатном сжатии (процесс , то адиабата идет круче изотермы. Объясняется это тем, что при адиабатном сжатии (процесс 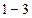 ) увеличение давления происходит не только за счет уменьшения объема, ) увеличение давления происходит не только за счет уменьшения объема, |
как при изотермическом сжатии, но и за счет увеличения температуры сжимаемого газа. При адиабатном расширении газа (процесс 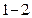 ) его температура уменьшается, и давление падает быстрее, чем при соответствующем изотермическом расширении.
) его температура уменьшается, и давление падает быстрее, чем при соответствующем изотермическом расширении.
Работа, совершаемая газом в адиабатном процессе 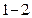
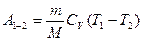 (2.3.26)
(2.3.26)
измеряется площадью, закрашенной на рис.3.6.
Из уравнения для внутренней энергии идеального газа  легко найти молярные теплоемкости
легко найти молярные теплоемкости 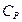 и
и 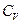 . Поскольку
. Поскольку  и
и  , то
, то
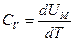
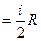 и
и 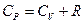 .
.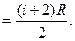 (2.3.29)
(2.3.29)
Соответственно, показатель адиабаты 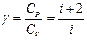 (2.3.30)
(2.3.30)
В табл.3.1 приведены значения 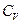 ,
, 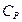 и
и 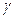 для идеальных газов с различными степенями свободы
для идеальных газов с различными степенями свободы
Таблица 3.1
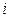 |  | 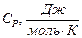 | 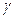 |
| 3 (одноатомный газ) | 12,5 | 20,8 | 1,67 |
| 5 (двухатомный газ) | 20,8 | 29,1 | 1,40 |
| 6 (многоатомный газ) | 24,9 | 33,2 | 1,33 |
Политропный процесс (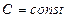 ) – термодинамический процесс, протекающий без изменения теплоемкости
) – термодинамический процесс, протекающий без изменения теплоемкости 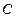 .
.
Уравнение политропы имеет вид: 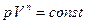 , (2.3.31)
, (2.3.31)
где 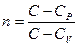 – показатель политропы (
– показатель политропы (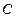 – теплоемкость газа в данном процессе).
– теплоемкость газа в данном процессе).
Все рассмотренные выше изопараметрические процессы являются частными случаями политропного процесса. Действительно, при 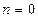 уравнение политропы описывает изобарный процесс (
уравнение политропы описывает изобарный процесс ( ). При
). При 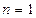 – изотермический процесс (
– изотермический процесс (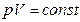 ). При
). При
 Рис.3.7 Рис.3.7 |
 это адиабатный процесс (
это адиабатный процесс (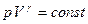 ). При
). При  уравнение политропы описывает изохорный процесс. В этом можно убедиться, если уравнение
уравнение политропы описывает изохорный процесс. В этом можно убедиться, если уравнение  , преобразовать к виду
, преобразовать к виду 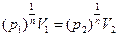 . При
. При 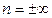 получаем
получаем  . Все эти процессы изображены на приведенной
. Все эти процессы изображены на приведенной 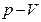 диаграмме (рис.3.7).
диаграмме (рис.3.7).
|
|
|
 2014-02-02
2014-02-02 9608
9608

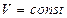 )
) )
)