2014-02-02
1608
Электрический ток – направленное движение носителей электрических зарядов. Если в данной среде происходит упорядоченное перемещение заряженных частиц под действием электрического поля, то ток называется током проводимости. Направление тока совпадает с направлением вектора напряжённости электрического поля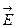 
. Сила тока – скалярная величина, численно равная количеству заряда, проходящего через сечение проводника за единицу времени, т.е.
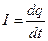. (3.8.1)
Если I = const, то такой ток называется постоянным. Единицей силы тока в СИ является ампер (А). Это одна из основных единиц системы СИ, которая устанавливается на основе закона взаимодействия двух токов. Еще одной важнейшей характеристикой тока считается его плотность, определяемая формулой:
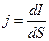, (3.8.2)
где dS – площадь, через которую проходит ток dI. В СИ i измеряется в (А/м2). Итак, наличие в данной среде свободных носителей электрических зарядов – заряженных частиц и электрического поля – необходимое условие для тока проводимости. Классическая элекутронная теория проводимости металлов, созданная П. Друде, затем развитая Г.Лоренцем, сумела получить основные законы электрического тока- законов Ома и Джоуля-Ленца, устновленных опытным путем. Формула закона Ома для плотности тока выглядит так:
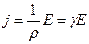, (3.8.3)
поскольку векторы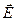 
и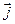 
имеют одинаковое направление можно последнюю формулу написать и так:
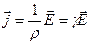. (3.8.4)
Затем закон Джоуля-Ленца для плотности тепловой мощности тока имеет вид:
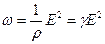. (3.8.5)
В этих формулах 
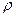– удельное сопротивление, 
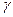– удельная проводимость. Из формул (3.8.3) и (3.8.5) можно перейти к интегральным формам записи законов Ома и Джоуля-Ленца.
Правила Кирхгофа для разветвлённых цепей.
Расчёт, встречающихся на практике сложных, разветвлённых цепей, значительно облегчается, если воспользоваться двумя правилами, установленными Кирхгофом.
Первое его правило относится к узлу – точке разветвлённой цепи, где сходятся не менее трёх проводников. Правило гласит: алгебраическая сумма сил токов, сходящихся в узле, равна нулю. При этом токи, подходящие к узлу, считаются положительными, отходящие от него – отрицательными. Это означает, что в узле не должно быть, также как в любой точке цепи постоянного тока, накопления зарядов. Поэтому должно иметь место равенство:
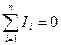, (3.8.6)
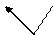
где n – число токов, сходящихся в узле. Для узла, приведённого на рис. 19.2, правило (3.8.6) запишется так: I1 – I2 + I3 - I4 + I5 = 0.
I2 I3
I1 I4
I5
Рис. 19.2
Второе правило относится к замкнутому контуру и гласит: в любом замкнутом контуре алгебраическая сумма произведений сил токов на сопротивление соответствующих участков равна алгебраической сумме э.д.с.. действующих в контуре, т.е.:
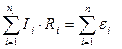, (3.8.7)
где n – число участков контура. При применении правила (3.8.7) выбирается направление обхода контура. Токи, направления которых совпадают с выбранным направлением, считаются положительными. Положительными также будут э.д.с., создающие ток, имеющий направление обхода контура. В качестве примера применения второго правила Кирхгофа рассмотрим замкнутый контур (рис. 19.3), состоящий из трёх участков.
 |
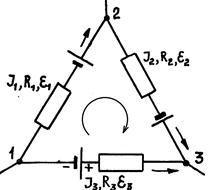Рис. 19.3
Пусть обход контура осуществляется по часовой стрелке. Тогда, согласно уравнения (3.8.7) имеет место равенство:
I1R1 + I2R2 – I3 R3 = ε1 + ε2 - ε3.
Другими примерами применения двух правил Кирхгофа, такими как, измерение сопротивлений проводников при помощи мостика Уитстона, определение э.д.с. методом компенсации – можно ознакомиться по ходу выполнения лабораторных работ.
