Лекция 9. Позволяет описать присущий многим системам элемент колебательности

Колебательное звено

Позволяет описать присущий многим системам элемент колебательности. Наиболее близкий математический аналог – математический маятник с фиксированным коэффициентом затухания.

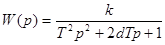
d – декремент затухания. Если d > 1, то T² p²+2dTp+1=(T₁p+1)(T₂p+1) следовательно, колебательное звено соответствует двум инерционным звеньям.

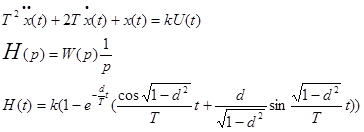
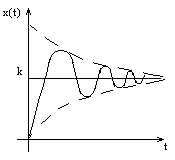
Если 0 Ј d Ј 1 – колебательное звено в полном смысле этого слова.

Колебательный переходный процесс с заданным затуханием. Где огибающая e^-dt/T

Все это справедливо при d < 1

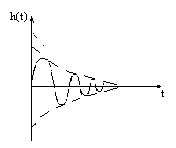
Весовая функция.

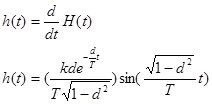
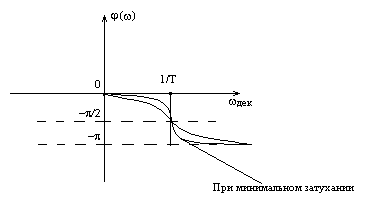
АФЧХ:

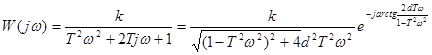
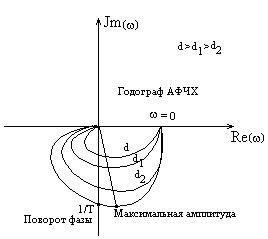
В зависимости от коэффициента затухания d, частотные характеристика колебательного звена может иметь максимум, если d < 0.707, или не иметь этого максимума, если d > 0.707

Это не что иное, как явление резонанса

А_макс=k/2d.

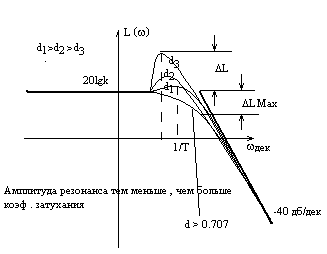
ЛАЧХ:

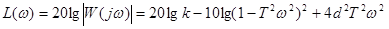
Рассматриваем область низких частот w << 1/T

L(w)» 20lgk

Область высоких частот w >> 1/T

L(w)» 20lgk-10lgT⁴w⁴=20lgk-10lgTw

Фаза никуда не смещается.

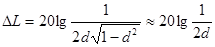
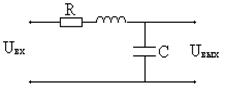
Реализация колебательного звена

Чем меньше d тем больше выражается резонанс, тем сильнее выражен скачок фазы.

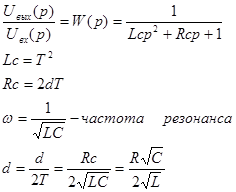
Таким образом, звено второго порядка имеет наклон LАЧХ ± 40 дб на декаду и максимальный поворот фазы ± p

Важнейший итог: любая передаточная функция может быть представлена в виде последовательного или параллельного соединения простейших типовых звеньев 1-го или 2-го порядка, каждое из которых даёт излом ЛАЧХ на +-20 или +- 40 дб/дек.

ФЧХ получают при этом приращение +- p/2 или +- p соответственно.