Замена переменных в двойном интеграле

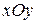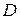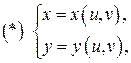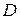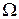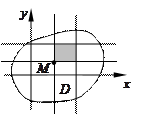
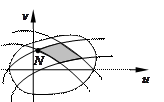
Пусть на плоскости задана область , заданы функции отображающие область в область на плоскости 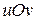(см. рисунок), причем точке 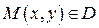соответствует точка 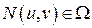, частичные прямоугольники в 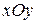отображаются в криволинейные
четырехугольники в плоскости .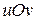

Предположим, что преобразование является непрерывным, дифференцируемым и взаимно обратным. Тогда можно найти функции 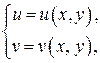определяющие обратное преобразование области в область 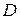, которые являются также непрерывными и дифференцируемыми, если не обращается в ноль определитель Якоби (якобиан) 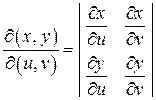, причем абсолютная величина якобиана 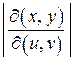задает коэффициент
искажения преобразования 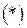и .

Поэтому при замене переменных 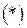с указанными свойствами в двойном интеграле следует применять формулу

.

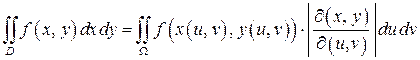Например, для перехода к полярным координатам 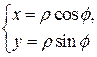якобиан 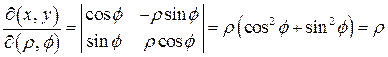, и поэтому при переходе к полярным координатам в двойном интеграле имеем

,

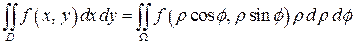здесь 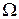– образ области 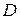рассматривается в полярных координатах.

Итак, для вычисления двойного интеграла нужно задать
область интегрирования неравенствами и перейти к повторному интегралу.