1). К цилиндрическим координатам целесообразно переходить, когда уравнение
поверхностей, ограничивающих тело, содержит 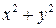 .
.
2). Внутреннее интегрирование обычно удобно вести по 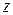 .
.
Пример 4. Вычислить массу тела, ограниченного поверхностями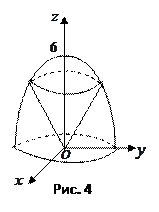
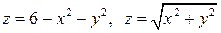 , если плотность
, если плотность 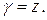
Решение. Поверхность  строим методом сечений:
строим методом сечений:
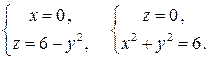 Получаем параболоид (рис. 4).
Получаем параболоид (рис. 4).
Поверхность 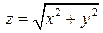 также строим методом сечений
также строим методом сечений
 Получаем конус (рис. 4).
Получаем конус (рис. 4).
В цилиндрической системе координат уравнения этих поверхностей имеют более простой вид: 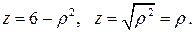 Решив систему из этих двух уравнений, найдем пересечение этих поверхностей ─ окружность
Решив систему из этих двух уравнений, найдем пересечение этих поверхностей ─ окружность 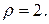
Вычислим массу тела, используя для вычисления интеграла цилиндрическую систему координат, учитывая, что 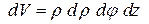 , внутреннее интегрирование ─ по
, внутреннее интегрирование ─ по 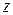 , причем на прямой, параллельной оси
, причем на прямой, параллельной оси 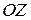 ,
, 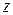 меняется от
меняется от 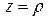 на конусе до
на конусе до 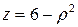 на поверхности параболоида (рис. 4):
на поверхности параболоида (рис. 4):
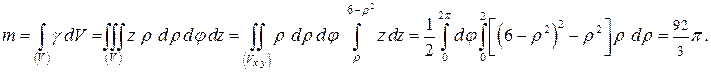
11. Лекционное занятие. ТРОЙНОЙ ИНТЕГРАЛ В СФЕРИЧЕСКИХ КООРДИНАТАХ
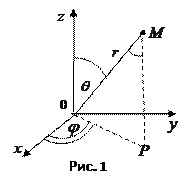 Положение точки
Положение точки 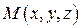 в пространстве можно охарактеризовать с помощью сферических координат
в пространстве можно охарактеризовать с помощью сферических координат 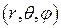 , где
, где  длина радиус-вектора точки
длина радиус-вектора точки 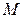 (рис. 1,
(рис. 1, 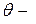 угол отклонения радиус-вектора точки
угол отклонения радиус-вектора точки 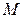 от оси
от оси 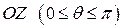 ,
, 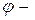 угол отклонения проекции на плоскость
угол отклонения проекции на плоскость 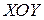 радиус-вектора точки
радиус-вектора точки 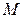 от оси
от оси 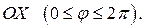
Установим связь между прямоугольными и сферическими координатами. Из прямоугольного треугольника 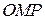 имеем
имеем 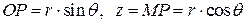 . Так как
. Так как 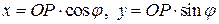 , то
, то
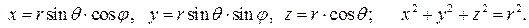
Вычислим якобиан
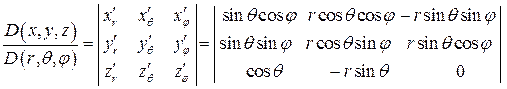 .
.
Раскроем определитель по элементам третьей строки
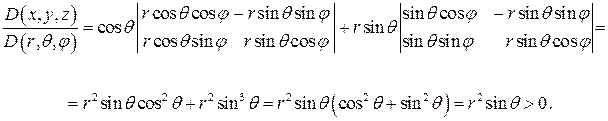
Тогда элемент объема в сферических координатах
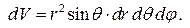
Для вычисления тройного интеграла следует
следует
1) заменить 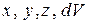 на их выражения в сферической системе координат,
на их выражения в сферической системе координат,

2) заменить область 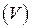 изменения переменных
изменения переменных 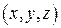 на область
на область 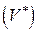 изменения переменных
изменения переменных 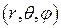 .
.
 2014-02-02
2014-02-02 1398
1398








