Для вычисления тройного интеграла иногда удобно использовать не прямоугольные координаты 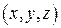 , а некоторые криволинейные координаты
, а некоторые криволинейные координаты 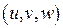 . Пусть известна связь между этими координатами
. Пусть известна связь между этими координатами
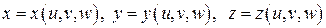 и
и 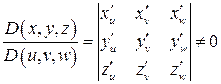 .
.
Аналогично случаю двойного интеграла можно показать, что
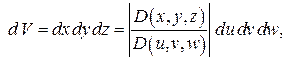

Здесь 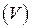 и
и 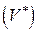 ─ области изменения соответственно переменных
─ области изменения соответственно переменных 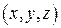 и
и 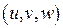 .
.
Для вычисления тройного интеграла следует
следует
1) заменить 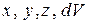 на их выражения в криволинейной системе координат,
на их выражения в криволинейной системе координат,
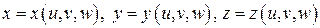 ,
, 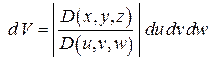 ;
;
2) заменить область 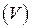 изменения переменных
изменения переменных 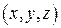 на область
на область 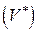 изменения переменных
изменения переменных 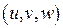 .
.
Замечание. Иногда удобнее вычислить не якобиан 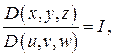 а якобиан
а якобиан 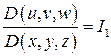 . Тогда искомый якобиан
. Тогда искомый якобиан 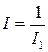 .
.
Пример 3. Вычислить объем параллелепипеда, ограниченного плоскостями
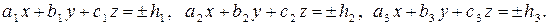
Решение. Введем новые переменные
 вычислим якобиан
вычислим якобиан 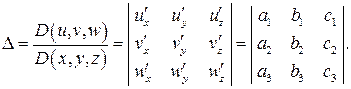
Тогда искомый объем равен
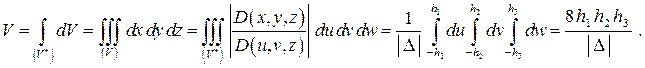
 2014-02-02
2014-02-02 757
757







