Совместимые понятия могут быть в отношениях равнозначности, пересечения и подчинения

Сравнимые понятия бывают

- совместимыми и

- несовместимыми.

Со­вместимыми называются понятия, объемы которых имеют общие эле­менты, каким-либо образом соприкасаются. Например, понятия спорт­смен и американец совместимые, так как их объемы имеют общие элементы, или объекты есть такие спортсмены, которые являются американцами и, наоборот, есть такие американцы, которые являются спортсменами.

Несовместимыми называются понятия, объемы которых не имеют общих элементов, никаким образом не соприкасаются. Напри­мер, понятия треугольник и квадрат являются несовместимыми, по­тому что их объемы не имеют общих элементов: ни один треугольник не может быть квадратом, и наоборот.

Понятия находятся в отношении равнозначности в том случае, если их объемы полностью совпадают.

Например, равнозначными будут понятия квадрат и равносторонний прямоугольник, так как любой квадрат — это равносторонний прямоугольник, а любой рав­носторонний прямоугольник — это квадрат. В логике принято изображать отношения между понятиями с помощью круговых схем Эй­лера (известный математик XVIII века): одно понятие, а вернее его объем, изображается одним кругом, а второе, т. е. его объем — дру­гим. Взаимное расположение этих кругов на схеме (они могут полно­стью совпадать или пересекаться, или не соприкасаться, или один круг располагается внутри другого) и показывает то или иное отно­шение между понятиями. Так, отношение равнозначности между по­нятиями квадрат и равносторонний прямоугольник изображается схемой (рис. 1), на которой два круга, обозначающие два равных объе­ма, полностью совпадают.

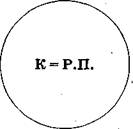
Рис. 1

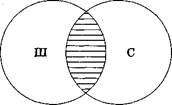
Рис. 2

Понятия находятся в отношении пересечения тогда, когда их объе­мы совпадают только частично. Например, пересекающимися будут по­нятия школьник и спортсмен, есть такие школьники, которые являют­ся спортсменами, и есть такие спортсмены, которые являются школь­никами; но в то же время школьник может не быть спортсменом, так же, как и спортсмен может не быть школьником. На схеме Эйлера отно­шение пересечения изображается двумя пересекающимися кругами (заштрихованная часть показывает частично совпадающие объемы двух понятий) (рис. 2).

Понятия находятся в отношении подчинения в том случае, когда объем одного из них обязательно больше объема другого и полностью его в себя включает (один объем как бы подчиняется другому). Например, в отношении подчинения находятся понятия карась и рыба, так как все караси — это обязательно рыбы, но рыбами являются не только караси, есть и другие виды рыб. Таким образом, объем понятия карась является меньшим по отношению к объему понятия рыба и полностью в него вклю­чается (подчиняется ему).

В отношении подчинения понятия с меньшим объемом называются видовыми, а с большим — родовыми. На схеме Эйлера отношение подчинения изображается двумя кругами, один из которых располагается внутри другого (рис. 3).

Отношениями равнозначности, пересечения и подчинения исчерпываются все случаи совместимости между понятиями.

Несовместимые понятия могут быть в отношениях соподчинения, противоположности и противоречия.

Понятия находятся в отношении соподчинения тогда, когда их объе­мы не имеют общих элементов, но в то же время входят в объем какого-то третьего понятия, родового для них (совместно ему подчиняются). Например, понятия сосна и береза являются соподчиненными: ни одна сосна не может быть березой, и наоборот, но и множество всех сосен, и множество всех берез включается в более широкий объем понятия дере­во. На схеме Эйлера отношение соподчинения изображается двумя не­соприкасающимися кругами (рис. 4

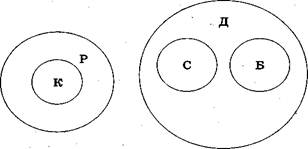
Рис.3 Рис.4

Понятия находятся в отношении противоположности в том случае, если они обозначают какие-то взаимоисключающие признаки, крайние состоя­ния чего-либо, между которыми, однако, всегда есть некий средний, пере­ходный вариант. Например, противоположными являются понятия высо­кий человек и низкий человек (третьим или переходным вариантом между ними будет понятие человек среднего роста). На схеме Эйлера отношение противоположности изображается двумя несоприкасающимся кругами, которые находятся как бы на разных «полюсах» (рис. 5).

Поскольку объемы противоположных понятий не соприкасаются, это отношение отчасти похоже на соподчинение. Однако понятия, находя­щиеся в отношении соподчинения, обозначают просто различные объек­ты разных видов и одного рода, но не противоположные друг другу. Не можем же мы утверждать, что сосна является противоположностью бе­резы, а береза — противоположностью сосны: это просто разные дере­вья, и не более того. В то же время высокий человек представляет собой противоположность низкого человека, и наоборот. Так же противопо­ложными будут понятия темная комната и светлая комната, горя­чая вода и холодная вода, белый лист и черный лист, глубокая речка и мелкая речка и т. п.

Понятия находятся в отношении противоречия, если одно из них представляет собой отрицание другого, причем в отличие от противоположных понятий, между противоречащими понятиями никак не может быть третьего или среднего варианта. Например, в отношении противоречия находятся понятия высокий человек и невысокий человек. В том случае, когда одно понятие является отрицанием другого, третий вари­ант автоматически исключается: и низкий человек, и человек среднего роста — это невысокий человек. На схеме Эйлера отношение противо­речия изображается одним кругом, поделенным на две части, которые обозначают противоречащие понятия (рис. 6).

Отношениями соподчинения, противоположности и противоречия исчерпываются все случаи несовместимости между понятиями.