Круговые схемы Эйлера

Как мы уже знаем, в логике выделяется шесть вариантов отношений между понятиями. Два любых сравнимых понятия обязательно на­ходятся в одном из этих отношений. Например, понятия писатель и россиянин находятся в отношении пересечения, писатель и человек — подчинения, город Москва и столица России — равнозначности, Москва и Петербург — соподчинения, мокрая дорога и сухая дорога — противо­положности, Антарктида и материк — подчинения, Антарктида и Африка — соподчинения и т. д. и т. п.

Надо обратить внимание на то, что если два понятия обозначают часть и целое, например месяц и год, то они находятся в отношении соподчине­ния, хотя может показаться, что между ними отношение подчинения, ведь месяц входит в год. Однако если бы понятия месяц и год были подчинен­ными, то тогда надо было бы утверждать, что месяц — это обязательно год, а год — это не обязательно месяц (вспомним отношение подчинения на примере понятий карась и рыба: карась — это обязательно рыба, но рыба — это не обязательно карась). Месяц — это не год, а год — это не месяц, но и то, и другое — отрезок времени, следовательно, понятия ме­сяц и год, так же, как и понятия книга и страница книги, автомобиль и колесо автомобиля, молекула и атом и т. п., находятся в отношении со­подчинения, так как часть и целое — не то же самое, что вид и род.

Вначале говорилось о том, что понятия бывают сравнимыми и несравнимыми. Считается, что рассмотренные шесть вариантов отноше­ний применимы только к сравнимым понятиям. Однако возможно ут­верждать, что все несравнимые понятия находятся между собой в отно­шении соподчинения. Например, такие несравнимые понятия, как пингвин и небесное тело возможно рассматривать как соподчиненные, ведь пингвин — это не небесное тело, и наоборот, но в то же время объе­мы понятий пингвин и небесное тело входят в более широкий объем тре­тьего понятия, родового по отношению к ним: это может быть понятие объект окружающего мира или форма материи (ведь и пингвин и не­бесное тело — это различные объекты окружающего мира или различ­ные формы материи). Если же одно понятие обозначает что-то материальное, а другое — нематериальное (например, дерево и мысль), то родо­вым для этих (как возможно утверждать) соподчиненных понятий является понятие форма бытия, так как и дерево, и мысль, и что угодно еще — это различные формы бытия.

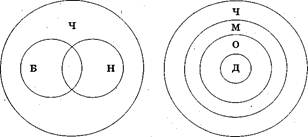
Рис. 7 Рис. 8

Как нам уже известно, отношения между понятиями изображаются круговыми схемами Эйлера. Причем до сих пор мы изображали схема­тично отношения между двумя понятиями, а это можно сделать и с боль­шим количеством понятий. Например, отношения между понятиями боксер, негр и человек изображаются следующей схемой (рис. 7).

Взаимное расположение кругов показывает, что понятия боксер и негр находятся в отношении пересечения (боксер может быть негром и мо­жет им не быть, а также негр может быть боксером и может им не быть), а понятия боксер и человек, так же как и понятия негр и человек нахо­дятся в отношении подчинения (любой боксер и любой негр — это обяза­тельно человек, но человек может не быть ни боксером, ни негром).

Рас­смотрим отношения между понятиями дедушка, отец, мужчина, чело­век с помощью круговой схемы (рис. 8).

Как видим, указанные четыре понятия находятся в отношении последовательного подчинения: дедушка — это обязательно отец, а отец — не обязательно дедушка; любой отец — это обязательно мужчина, однако не всякий мужчина является отцом; и, наконец, мужчина — это обяза­тельно человек, но человеком может быть не только мужчина.

Отноше­ния между понятиями хищник, рыба, акула, пиранья, щука, живое су­щество изображаются следующей схемой (рис. 9).

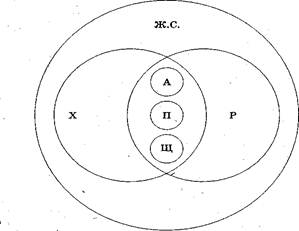
Рис.9

Попробуйте самостоятельно прокомментировать эту схему, установив все имеющиеся на ней виды отношений между понятиями.

Подытоживая сказанное, отметим, что отношения между понятия­ми — это отношения между их объемами. Значит, для того чтобы было возможно установить отношения между понятиями, их объем должен быть четким, а содержание, соответственно, ясным, т. е. эти понятия должны быть определенными. Что касается неопределенных понятий, о которых шла речь выше, то установить точные отношения между ними достаточно сложно, фактически невозможно, ведь из-за неясности их содержания и нечеткости объема два каких-нибудь неопределенных понятия можно будет характеризовать как равнозначные или как пере­секающиеся, или как подчиняющиеся и т. д. Например, возможно ли установить отношения между неопределенными понятиями неаккурат­ность и небрежность? То ли это будет равнозначность, то ли подчине­ние — точно сказать невозможно. Таким образом, отношения между неопределенными понятиями являются так же неопределенными. По­нятно поэтому, что в тех ситуациях интеллектуально-речевой практи­ки, где требуется точность и однозначность в определении отношений между понятиями, использование неопределенных понятий является нежелательным.

2.3. Как ограничивать и обобщать понятия?

Среди различных видов отношений между понятиями следует об­ратить особенное внимание на подчинение. Как уже говорилось, поня­тия с меньшим объемом называются видовыми, а понятия с большим объемом — родовыми, причем объем видового понятия всегда полнос­тью включается в объем родового. Видовые и родовые понятия тесно связаны между собой логическими операциями ограничения и обоб­щения.

Ограничение понятия — это логическая операция перехода от родового понятия к видовому с помощью прибавления к его содержанию какого-либо признака.

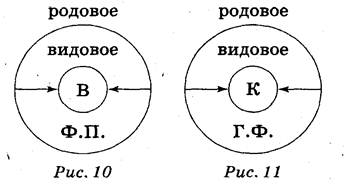
Вспомним об обратном отношении между объемом и содержанием понятия: чем больше объем, тем меньше содержание, и наоборот. Ограничение понятия или переход от родового понятия к ви­довому — это уменьшение его объема, а значит — увеличение содержа­ния. Вот почему при добавлении каких-то признаков к содержанию по­нятия автоматически уменьшается его объем. Например, если к содер­жанию понятия физический прибор прибавить признак измерять напряжение электрического тока, то оно превратится в понятие вольт­метр, которое будет видовым по отношению к исходному родовому по­нятию физический прибор (рис. 10).

Так же, если к содержанию понятия геометрическая фигура прибавить признак иметь равные стороны и прямые углы, то оно превратится в понятие квадрат, которое будет видовым по отношению к исходному родовому понятию геометрическая фигура (рис. 11).

Обобщение понятия — это логическая операция, которая противоположна ограничению и представляет собой переход от видового поня­тия к родовому с помощью отбрасывания от его содержания какого-либо признака.

Понятно, что содержание понятия, лишенное каких-то при­знаков, уменьшается, но при этом автоматически увеличивается объем понятия, которое из видового становится родовым или обобщается. На­пример, если от содержания понятия биология отбросить признак изу­чать различные формы жизни, то оно превратится в понятие наука, которое будет родовым по отношению к исходному видовому понятию биология (рис. 12).

Так же, если от содержания понятия атом водорода отбросить признак иметь один электрон, то оно превратится в понятие атом химического элемента, которое будет родовым по отношению к исходному видовому понятию атом водорода (рис. 13).