Цепочки ограничений и обобщений понятий

Ограничения и обобщения понятий складываются в логические це­почки, в которых каждое понятие (за исключением начального и конеч­ного) является видовым по отношению к одному соседнему понятию и родовым по отношению к другому. Например, если последовательно обобщать понятие Солнце, то получится следующая цепочка:

Солнце —> звезда —> небесное тело —> физическое тело —>форма материи.

В этой цепочке, как видим, понятие звезда является родовым по отношению к понятию Солнце, но видовым по отношению к понятию небес­ное тело; так же понятие небесное тело является родовым по отноше­нию к понятию звезда, но видовым по отношению к понятию физиче­ское тело и т. д. Понятно, что движение по нашей цепочке от понятия Солнце к понятию форма материи представляет собой серию последо­вательных обобщений, а движение в обратном направлении — ограни­чений. Если изобразить отношения между понятиями из указанной це­почки на схеме Эйлера, то получатся круги, последовательно распола­гающиеся один в другом: самый маленький соответствует понятию Солнце, а самый большой — форма материи.

Пределом цепочки ограничения любого понятия всегда будет какое-либо единичное понятие, а пределом цепочки обобщения, как правило, будет какое-либо широкое, философское понятие (например, объект мироздания, форма материи или форма бытия).

Наиболее частые ошибки, которые допускают при ограничении и обобщении понятий, заключаются в том, что вместо вида для какого-то рода называют часть из некоего целого, и вместо рода для какого-то вида называют целое по отношению к какой-либо части.

Например, в каче­стве ограничения понятия цветок предлагают понятие стебель. Стебель, конечно, является частью цветка, но ограничить понятие — это значит подобрать не часть для целого, а вид для рода, т. е. правильным ограни­чением понятия цветок будет понятие ромашка, или тюльпан, или хри­зантема и т. п.

Так же, например, в качестве обобщения понятия дере­во нередко предлагают понятие лес. Конечно, лес является неким целым по отношению к деревьям, из которых он состоит, но обобщить поня­тие — это значит подобрать не целое для части, а род для вида, т. е. пра­вильным обобщением понятия дерево будет понятие растение, или объект флоры, или живой организм и т. п.

Итак, почти любое понятие можно как ограничить, так и обобщить. Это значит подобрать для него как видовое понятие, так и родовое. На­пример, ограничением понятия человек будет понятие спортсмен (или писатель, или мужчина, или молодой человек и т. п.), а его обобщением будет понятие живое существо (рис. 14).

Выше было сказано, что ограничить и обобщить можно почти любое по­нятие. Правильнее было бы утверждать, что подавляющее большинство понятий можно подвергнуть логическим операциям ограничения и обобщения. Какие же понятия невозможно ограничить или обобщить? Мы их уже упоминали — это единичные понятия или широкие, философ­ские понятия, на которых заканчивается любая логическая цепочка

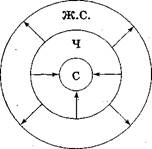
Рис. 14

ограничения или обобщения. Единичные понятия невозможно ограни­чить (однако их можно последовательно, поэтапно обобщать вплоть до какого-то широкого, философского понятия), а философские, предель­но широкие по объему понятия невозможно обобщить (но их можно по­следовательно ограничивать вплоть до какого-то единичного понятия).

3. Логические операции определения, деления, сложения и умножения понятий