Характеристическое уравнение имеет два различных действительных корня

2.

1.

Переходим к рассмотрению дифференциальных уравнений второго порядка и дифференциальных уравнений высших порядков. Многие принципы решения и базовые понятия диф.уравнений первого порядка автоматически распространяются и на дифференциальные уравнения высших порядков.

Наиболее популярны дифференциальные уравнения второго порядка. В дифференциальное уравнение второго порядка обязательно входит вторая производная 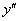и не входят производные более высоких порядков:

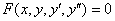
Следует отметить, что 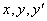(и даже все сразу) могут отсутствовать в уравнении, важно, чтобы был 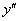. Самое примитивное дифференциальное уравнение второго порядка выглядит так: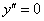

В дифференциальное уравнение третьего порядка обязательно входит третья производная 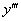и не входят производные более высоких порядков:

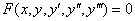
Самое простое дифференциальное уравнение третьего порядка выглядит так: 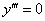– Аналогичным образом можно определить дифференциальные уравнения 4-го, 5-го и более высоких порядков. Дифференциальные уравнения высших порядков, которые предлагаются в практических задачах, можно разделить на две основные группы.

1) Первая группа – так называемые уравнения, допускающие понижение порядка.(СР)

2) Вторая группа – линейные уравнения высших порядков с постоянными коэффициентами.

В теории и практике различают два типа таких уравнений – однородное уравнение и неоднородное уравнение.

Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:
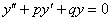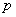, где и 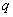– константы (числа), а в правой части – нуль.

Неоднородное ДУ второго порядка с постоянными коэффициентами имеет вид:
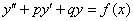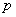, где и 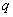– константы, а 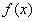– функция, зависящая только от «икс». В простейшем случае функция 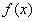может быть числом, отличным от нуля.

Чтобы научиться решать неоднородные уравнения необходимо уметь решать однородные уравнения. По этой причине сначала рассмотрим алгоритм решения линейного однородного уравнения второго порядка:

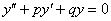
Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:

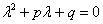
По какому принципу составлено характеристическое уравнение, отчётливо видно:
вместо второй производной записываем ;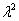
вместо первой производной записываем просто «лямбду»;
вместо функции 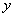ничего не записываем.

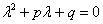– это обычное квадратное уравнение, которое предстоит решить.

Существуют три варианта развития событий.
Они доказаны в курсе математического анализа, и на практике мы будет использовать готовые формулы.

Если характеристическое уравнение 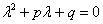имеет два различных действительных корня 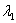, 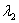(т.е., если дискриминант 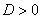), то общее решение однородного уравнения выглядит так:
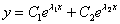, где 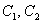– константы.

В случае если один из корней равен нулю, решение очевидным образом упрощается; пусть, например, 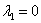, тогда общее решение: .

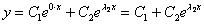Пример 1

Решить дифференциальное уравнение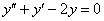

Решение: составим и решим характеристическое уравнение:

,
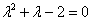
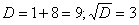
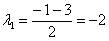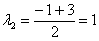
Получены два различных действительных корня.
Всё, что осталось сделать – записать ответ, руководствуясь формулой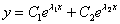

Ответ: общее решение: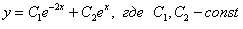

Не будет ошибкой, если записать общее решение наоборот: 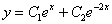, но хорошим стилем считается располагать коэффициенты по возрастанию, сначала –2, потом 1.

Придавая константам 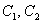различные значения, можно получить бесконечно много частных решений.

А что значит вообще решить дифференциальное уравнение? Решить дифференциальное уравнение – это значит найти множество решений, которое удовлетворяет данному уравнению. Такое множество решений называется общим интегралом или общим решением дифференциального уравнения.

Таким образом, в рассмотренном примере найденное общее решение 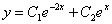должно удовлетворять исходному уравнению 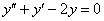. Точно так же, как и в ДУ 1-го порядка, в большинстве случаев легко выполнить проверку:

Берем наш ответ 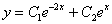и находим производную:

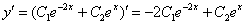
Находим вторую производную:

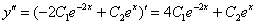
Подставляем 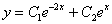, 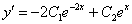и 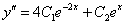в левую часть уравнения :

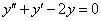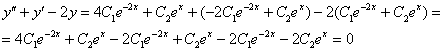
Получена правая часть исходного уравнения (ноль), значит, общее решение 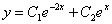найдено правильно (оно, как проверено, удовлетворяет уравнению ).

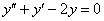Пример 2

Найти общее решение дифференциального уравнения, выполнить проверку

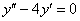
Это пример для самостоятельного решения, полное решение и ответ в конце урока.

На самом деле проверка таких простейших примеров практически никогда не выполняется, но, дело в том, что навык и сама техника проверки очень пригодятся, когда вы будете решать более сложные неоднородные уравнения второго порядка. Поэтому было целесообразно сразу же ознакомить вас с алгоритмом.