Системы линейных дифференциальных уравнений.
Такая система имеет вид
 (7)
(7)
Мы предполагаем, что коэффициенты 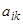 непрерывны на интервале
непрерывны на интервале 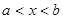 .
.
Пусть частным решением системы (7) является система функций 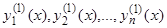 , так что при подстановке в уравнения (7) эти функции обращают их в тождества. В таком случае система функций
, так что при подстановке в уравнения (7) эти функции обращают их в тождества. В таком случае система функций 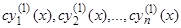 также является решением системы (7). Далее, если
также является решением системы (7). Далее, если 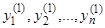 и
и 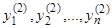 — два частных решения, то
— два частных решения, то 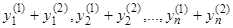 также является решением системы (7). Как следствие, можно заключить, что линейная комбинация с произвольными постоянными коэффициентами решений однородной линейной системы является решением той же системы.
также является решением системы (7). Как следствие, можно заключить, что линейная комбинация с произвольными постоянными коэффициентами решений однородной линейной системы является решением той же системы.
Пусть мы имеем  частных решений
частных решений
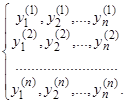 (8)
(8)
Назовем систему решений (8) фундаментальной, если определитель
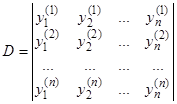 (8.1)
(8.1)
не равен тождественно нулю на интервале 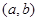 . Фактически, определитель
. Фактически, определитель 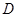 представляет собой определитель Вронского. Фундаментальные системы существуют: достаточно взять
представляет собой определитель Вронского. Фундаментальные системы существуют: достаточно взять 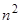 чисел
чисел 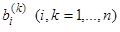 таких, чтобы их определитель
таких, чтобы их определитель 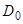 был не равен нулю. Затем определим
был не равен нулю. Затем определим  частных решений
частных решений 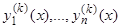 , принимающих при
, принимающих при 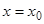 начальные значения
начальные значения 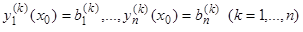 . Здесь
. Здесь 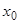 — некоторая точка интервала
— некоторая точка интервала 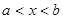 . Тогда, в силу непрерывности функций
. Тогда, в силу непрерывности функций 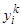 , определитель
, определитель 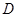 будет отличен от нуля также в некотором интервале, окружающем точку
будет отличен от нуля также в некотором интервале, окружающем точку 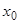 . Мы можем доказать больше.
. Мы можем доказать больше.
Теорема. Если 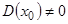 , то
, то 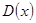 не обращается в 0 ни в какой точке интервала
не обращается в 0 ни в какой точке интервала 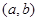 .
.
Для доказательства вычислим производную  . Дифференцируем по столбцам:
. Дифференцируем по столбцам:
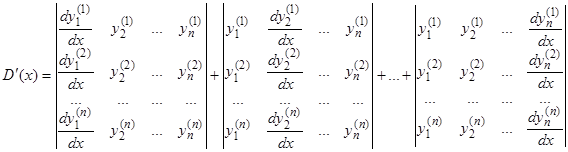 .
.
Заменив в каждом определителе в правой части производные 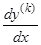 их выражениям из уравнений (7), мы получим, например, для первого слагаемого:
их выражениям из уравнений (7), мы получим, например, для первого слагаемого:
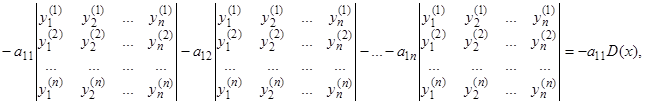 так как все определители, кроме первого, имеют два равных столбца. Аналогично, второе слагаемое дает
так как все определители, кроме первого, имеют два равных столбца. Аналогично, второе слагаемое дает 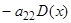 , …,
, …,  -е слагаемое дает
-е слагаемое дает 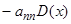 . Итак, имеем
. Итак, имеем 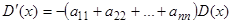 , или
, или 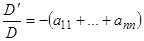 , откуда
, откуда 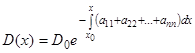 . Следовательно, если
. Следовательно, если 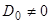 , то
, то 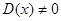 на всем интервале, где коэффициенты
на всем интервале, где коэффициенты 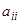 (а следовательно, и решения) непрерывны, т.е. на интервале
(а следовательно, и решения) непрерывны, т.е. на интервале 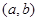 .
.
Теорема. Если 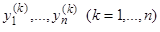 образуют фундаментальную систему частных решений системы (7), то общее решение будет выглядеть так:
образуют фундаментальную систему частных решений системы (7), то общее решение будет выглядеть так:
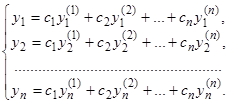 (9)
(9)
Мы видим, что формулы (9) представляют собой решение системы. Чтобы доказать, что это решение общее, нужно показать, что постоянные  можно определить так, что функции
можно определить так, что функции 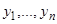 будут при
будут при 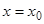 удовлетворять начальным условиям
удовлетворять начальным условиям 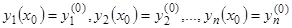 , где
, где 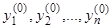 — любые числа. Подставляя эти условия в выражения (9), мы получим для определения
— любые числа. Подставляя эти условия в выражения (9), мы получим для определения  систему
систему  линейных алгебраических уравнений
линейных алгебраических уравнений
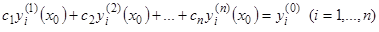 . (10)
. (10)
Так как, по доказанному, 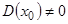 , то система (10) имеет определенную систему решений
, то система (10) имеет определенную систему решений  . Подставляя в формулы (9) найденные значения произвольных постоянных, мы и получим искомое частное решение. Теорема доказана.
. Подставляя в формулы (9) найденные значения произвольных постоянных, мы и получим искомое частное решение. Теорема доказана.
Естественно ввести определение линейной независимости системы функций. Систему функций вида (8) мы назовем линейно независимой, если не существует такой системы постоянных чисел 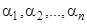 (которые не все равны нулю), что имели бы место на интервале
(которые не все равны нулю), что имели бы место на интервале 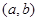
 тождеств:
тождеств:
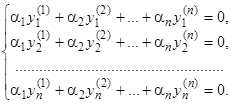 (11)
(11)
В противном случае система функций (8) называется линейно зависимой.
Отметим следующий факт: для  функций, дающих решение системы линейных дифференциальных уравнений, понятия фундаментальной системы и линейно независимой системы совпадают (вообще-то, требует доказательства).
функций, дающих решение системы линейных дифференциальных уравнений, понятия фундаментальной системы и линейно независимой системы совпадают (вообще-то, требует доказательства).
Задача построения системы линейных уравнений, имеющих заданную систему решений
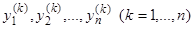 (8)
(8)
решается следующими формулами:
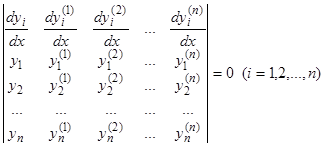 .
.
Заметим, что коэффициентом при производных 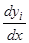 является
является  , определенный формулой (8.1). Если
, определенный формулой (8.1). Если  не обращается в нуль на интервале
не обращается в нуль на интервале 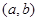 , то, деля на
, то, деля на  , получаем линейную систему уравнений в нормальной форме.
, получаем линейную систему уравнений в нормальной форме.
Пример. Найти линейную однородную систему второго порядка, допускающую следующую систему уравнений:

Искомые уравнения будут:
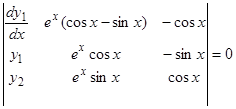 ,
,
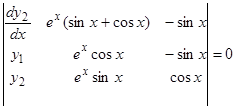 ,
,
или, раскрывая определители по первому столбцу и деля оба уравнения на 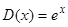 , получаем искомую систему:
, получаем искомую систему:
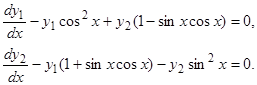
Систему линейных дифференциальных уравнений часто записывают в сокращенной форме:
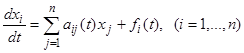 (12)
(12)
или в векторной форме
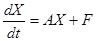 , (13)
, (13)
где 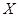 есть
есть  -мерный вектор с координатами
-мерный вектор с координатами 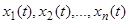 ,
, 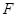 есть
есть  -мерный вектор с координатами
-мерный вектор с координатами 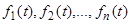 . Удобно рассматривать их как одностолбцовые матрицы.
. Удобно рассматривать их как одностолбцовые матрицы.
Определим линейный оператор 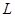 равенством
равенством  , тогда уравнение (13) еще короче можно записать в виде
, тогда уравнение (13) еще короче можно записать в виде
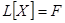 . (14)
. (14)
Линейная однородная система, таким образом, в краткой записи имеет вид
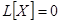 . (15)
. (15)
Оператор 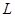 обладает следующими двумя свойствами:
обладает следующими двумя свойствами:
1) 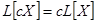 , где
, где  — произвольная постоянная.
— произвольная постоянная.
2) 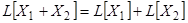 .
.
Следствием этих свойств является  .
.
Теорема. Если линейная однородная система (15) с действительными коэффициентами  имеет комплексное решение
имеет комплексное решение 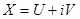 , то действительная и мнимая части
, то действительная и мнимая части  и
и 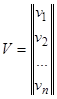 в отдельности являются решениями той же системы.
в отдельности являются решениями той же системы.
Доказательство. Дано 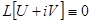 . Надо доказать, что
. Надо доказать, что 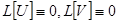 . Пользуясь свойствами 1) и 2) оператора
. Пользуясь свойствами 1) и 2) оператора 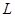 , получаем
, получаем 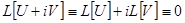 . Следовательно,
. Следовательно, 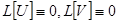 .
.
 2014-02-02
2014-02-02 1078
1078
