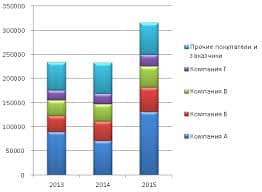
Теорема Лагранжа о конечных приращениях
Теорема Ролля о нуле производной
Теорема. Если f непрерывна на [ a,b ], дифференцируема на (a,b) и f (a) =f (b). Тогда $ x 0Î(a,b): f¢ (x 0)=0.
Доказательство. Положим,
. Хотя бы одна из точек x 1, x 2 будет внутренней () и для этой точки утверждение следует из теоремы Ферма.
Рис. 4.14
Теорема. Если f непрерывна на [ a,b ], дифференцируема на (a,b), то
$xÎ(a,b): f (b) -f (a) =f¢ (x)(b-a).
Доказательство. Рассмотрим функцию
. Для этой функции F (a) =F (b) = 0, и к ней применима теорема Ролля
.
Существует точка, касательная в которой, параллельна хорде, соединяющей точки A и B графика функции.
Рис. 4.15
Следствие 1. Если f непрерывна на [ a,b ], дифференцируема на (a,b) и f¢ (x)º0 на (a,b), то f (x)ºconst.
Применяя теорему к произвольному отрезку [ a,x ], где x произвольная фиксированная точка, получим f (x) - f (a) =f¢ (x)(x - a)=0, т.е. f (x) = f (a).
Следствие 2. Если f непрерывна на [ a,b ], дифференцируема на (a,b) и f¢ (x) =g¢ (x) на (a,b), то f (x) =g (x) + const.
Теорема. Если f, g непрерывны на [ a,b ], дифференцируемы на (a,b), то существует xÎ(a,b) такая, что
.
Доказательство. Рассмотрим вспомогательную функцию
F (x) = g (x)(f (b) - f (a)) - f (x)(g (b) - g (a)).
Для этой функции будет выполнено
F (a) = g (a)(f (b) - f (a)) - f (a)(g (b) - g (a)) = g (a) f (b) - f (a) g (b),
F (b) = g (b)(f (b) - f (a)) - f (b)(g (b) - g (a)) = - f (a) g (b) +g (a) f (b), таким образом, F (a) =F (b)
и к этой функции применима теорема Ролля:существует точка xÎ(a,b)для которой выполняется равенство
0 =F (b) -F (a) =F¢ (x)(b-a) = [ g¢ (x)(f (b) -f (a)) -f¢ (x)(g (b) -g (a))](b-a).
Следствие. Если g¢ (x)¹0 на (a,b), то.
Доказательство. Если g¢ (x)¹0, то g (b) -g (a) ¹0. Иначе, в случае g (b) =g (a), по теореме Ролля нашлась бы точка x, где g¢ (x)=0.
4.4 Правило Лопиталя
Раскрытие неопределенностей при вычислении пределов.
4.4.1.Раскрытие неопределенностей вида 0/0
Дано: f (x), g (x) определены на (x 0, b) и
1)
2) f, g дифференцируемы на (x 0, b).
3) g¢ (x)¹0 на (x 0, b).
Тогда, если существует конечный или бесконечный предел.
Доказательство. Доопределим функции f и g в точке x 0 по непрерывности нулем: f (x 0) =g (x 0)=0. По теореме Коши, примененной к отрезку [ x 0, x ], будет существовать x(x): x 0 < x(x) < x и, из условия x 0 < x(x) <x следует, что, причем x(x)¹ x 0, если x ¹ x 0. Тогда. Последнее равенство справедливо по теореме о существовании предела суперпозиции, ч.т.д.
Замечание. Аналогично, это утверждение доказывается для левой окрестности. Откуда получаем утверждение для x® x 0.
Следствие 1. Если
1) Существуют f (k) ,g (k), k= 1,2, …,n на (x 0 ,b).
2), k= 0,1 ,…,n -1.
3) Существуeт g (n)(x)¹0 на (x 0 ,b), то
еслисуществует, конечный или бесконечный.
Следствие 2. Если f, g дифференцируемы для x>a,,то
если последний существует, конечный или бесконечный.
Доказательство. Сделаем замену
Замечание. Аналогичные утверждения имеют место для x® -¥.
4.4.2.Раскрытие неопределенностей вида ¥/¥
f,g определены на (x 0, b) и
1).
2) f, g дифференцируемы на (x 0 ,b).
3) g¢ (x)¹0 на (x 0, b).
Тогда, если последний существует конечный или бесконечный.
Без доказательства.
Замечание. Аналогичные утверждения имеют место для x® x 0 - 0, x® x 0, x® + ¥, x® - ¥.
4.4.3.Использование правила Лопиталя для выделения главных частей и определения порядков бесконечно больших
В некоторых случаях порядок бесконечно малой или бесконечно большой можно определить, последовательно вычисляя производные. Предположим, что f (x) – бесконечно малая при x® x 0и в точке x 0обращаются в ноль все производные до (n -1) - го порядка включительно f (x 0)=0, f¢ (x 0)=0, …, и. В этом случае порядок этой бесконечно малой будет равен n. При этом главная часть будет равна. Это утверждение следует из равенства, в котором в качестве функции g (x)берется (x-x 0) n.
.
Похожее утверждение можно сформулировать и для бесконечно больших функций.
Пример: Выделить главную часть функции
f (x) = 3sh x - 3sin x – x 3при x® 0.
f ¢(x) = = 0, f¢¢(x)= = 0,
f¢¢¢(x)= = 0, f (4)(x) = = 0,
f (5)(x) = = 0, f (6)(x) = = 0,
f (7)(x) = = 6¹0.
Таким образом, порядок этой бесконечно малой равен 7 и f (x) ~ x 7=, x® 0.
4.4.4.Раскрытие неопределенностей вида 0¥, 1¥ , 00, ¥0, ¥ - ¥
Неопределенности вида 0¥ сводятся к уже рассмотренным ранее.
Примеры.
1).
2).
3).
4) ¥ - ¥
.
Можно, например, так
5) Неопределенности вида 1¥, 00, ¥0 сводятся к уже рассмотренным ранее логарифмированием
y=uv=ev ln u
Пример1..Вычисление.. Этот предел рассматриваем, как, где, а. Из теоремы о существовании предела суперпозиции двух функций следует, что. Далее, заменяя знаменатель на эквивалентную бесконечно малую получим:
= =
=. Таким образом,.
Пример 2.. Представим функцию в следующем виде: и вычислим предел
4.5 Формула Тейлора
Формула Тейлора. Различные остатки в формуле Тейлора.
4.5.1.Многочлен Тейлора. Формула Тейлора с остаточным членом Rn
Пусть у функции f существует f(n) (x 0) (это предпологает существование всех производных до (n -1) - го порядка в некоторой окрестности U= (x 0 -a,x 0 +a) точки x 0). Многочленом Тейлора в точке x 0 называется многочлен вида
Производные многочлена Тейлора будут равны:
(1)
Из (1) следует
= (2)
В частности, из дифференцируемости функции в точке получаем:
=. (3)
Далее, из (1) получается замечательное свойство многочлена Тейлора: он имеет в точке такие же производные, что и сама функция до порядка включительно («нулевая производная» - это сама функция):
Pn (x 0) =f (x 0), (4)
В частности,, k= 0,1, …,n -1.
Обозначим Rn (x) =f (x) - Pn (x), тогда
(5)
Выражение (5) называется формулой Тейлора функции f в окрестности точки x 0 с остаточным членом Rn. Основная задача будет состоять в представлении остатка в удобной для оценок форме.
Пример. Для функции найти многочлен, имеющий такие же прозводные в точке, что и, до 5-го порядка включительно.
 2014-02-02
2014-02-02 958
958